Definición y tipos

De Wikillerato

Revisión de 10:48 26 sep 2010 (editar) Fjmolina (Discutir | contribuciones) ← Ir a diferencias anteriores		Revisión de 16:39 27 sep 2010 (editar) (deshacer) Fjmolina (Discutir | contribuciones) Ir a las siguientes diferencias →
Línea 1:		Línea 1:
		+
		+	==Introducción==
		+
	<br/>		<br/>
-	==Definición==	+	Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones.
	<br/>		<br/>
-	Un '''''sistema de ecuaciones lineales''''' con incógnitas &nbsp;	+	Los métodos de [[Métodos de resolución de sistemas de ecuaciones lineales#Método de igualación|igualación]], [[Métodos de resolución de sistemas de ecuaciones lineales#Método de sustitución|sustitución]] y [[Métodos de resolución de sistemas de ecuaciones lineales#Método de reducción|reducción]] consisten en
-	<math>	+	encontrar y resolver, para cada una de las incognitas, una ecuación con esa
-	\left(	+	incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas
-	\, x_1, \, x_2, \, \ldots, \, x_n \,	+	facil, ¿no?).
-	\right)	+
-	</math>	+
-	&nbsp; es un conjunto formado por &nbsp;	+
-	<math>	+
-	m	+
-	</math>	+
-	&nbsp; igualdades de la forma:	+
	<br/>		<br/>
		+	A estas ecuaciones, con solo una incognita, se llega a traves de una serie de
		+	pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos
		+	incognitas que las ecuaciones previas.
		+
		+	<br/>
		+
		+	Así, es posible que en uno de estos pasos de eliminación de incognitas se utilize
		+	un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se
		+	utilize otro método ( el de igualación, por ejemplo ).
		+
		+	<br/>
		+
		+	Cada vez que se encuentra la solución para una incognita, se sustituye esta
		+	incognita por su solución para obtener asi ecuaciones con menos incognitas.
		+
		+	<br/>
		+
		+	Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar
		+	para resolver [[Definición y tipos#Sistemas de ecuaciones lineales compatibles determinados|sistemas de ecuaciones compatibles determinados]] e
		+	[[Definición y tipos#Sistemas de ecuaciones lineales compatibles indeterminados|indeterminados]].
		+
		+	<br/>
		+
		+	Estos mismos métodos tambien pueden utilizarse para comprobar si un sistema de
		+	ecuaciones es compatible o no. La utilizacion de cualquiera de ellos
		+	conduciria, en el caso de que el sistema fuese incompatible, a una igualdad que
		+	es falsa, por ejemplo:
	<center>		<center>
	<math>		<math>
-	\left.	+	2 = 3
-	\begin{array}{c}	+
-	a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1	+
-	\\	+
-	a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2	+
-	\\	+
-	\dotfill	+
-	\\	+
-	a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m	+
-	\end{array}	+
-	\right\}	+
	</math>		</math>
	</center>		</center>
Línea 37:		Línea 50:
	<br/>		<br/>
-	donde los &nbsp;	+	El [[Métodos de resolución de sistemas de ecuaciones lineales#Método de la matriz inversa|método de la matriz inversa]] y la [[Métodos de resolución de sistemas de ecuaciones lineales#Regla de Cramer|regla de Cramer]] solo se pueden utilizar en
		+	el caso de que el sistema de ecuaciones lineales sea compatible determinado.
		+
		+	<br/>
		+
		+	==Método de reducción==
		+
		+	<br/>
		+
		+	Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número
		+	de incognitas hasta llegar a ecuaciones con solo una incognita.
		+
		+	<br/>
		+
		+	Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de
		+	la ecuación por dicho número.
		+
		+	<br/>
		+
		+	Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho
		+	( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las
		+	ecuaciones que se suman.
		+
		+	<br/>
		+
		+	===Ejemplo===
		+
		+	<br/>
		+
		+	<center>
	<math>		<math>
-	a_{ij}	+	\left\{
		+	\begin{array}{l}
		+	5x - 3y = 2
		+	\\
		+	3x - 4y = -1
		+	\end{array}
		+	\right.
	</math>		</math>
-	&nbsp; se llaman '''''coeficientes''''' y los &nbsp;	+	</center>
		+
		+	Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones
		+	<center>
	<math>		<math>
-	b_i	+	\left\{
		+	\begin{array}{l}
		+	15x - 9y = 6
		+	\\
		+	-15x + 20y = 5
		+	\end{array}
		+	\right.
	</math>		</math>
-	, &nbsp; '''''terminos independientes''''' del sistema.	+	</center>
-	<br/>	+	El sumar ambas ecuaciones nos da la ecuación
-		+	<center>
-	En los coeficientes &nbsp;	+
	<math>		<math>
-	a_{ij}	+	11y = 11
	</math>		</math>
-	, &nbsp; el subindice &nbsp;	+	</center>
		+	que es una ecuación con una sola incognita y cuya solución es
		+	<center>
	<math>		<math>
-	i	+	y = 1
	</math>		</math>
-	&nbsp; indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice	+	</center>
-	&nbsp;	+	La elección de los factores 3 y -5 se ha hecho precisamente para que la
	<math>		<math>
-	j	+	x
	</math>		</math>
-	&nbsp; se&ntilde;ala de que incognita es coeficiente &nbsp;	+	desaparezca al sumar ambas ecuaciones.
		+
		+	<br/>
		+
		+	Sutituyendo <math> y </math> por uno en la primera ecuación del sistema de
		+	ecuaciones de partida, se obtiene
		+	<center>
	<math>		<math>
-	a_{ij}	+	5x - 3 = 2
	</math>		</math>
-	.	+	</center>
		+	que es otra ecuación con una sola incognita y cuya solución es &nbsp;
		+	<math>
		+	x = 1
		+	</math>.
	<br/>		<br/>
-	El subindice &nbsp;	+	==Método de igualación==
		+
		+	<br/>
		+
		+	El método de igualación consiste en lo siguiente:
		+
		+	<br/>
		+
		+	Supongamos que tenemos dos ecuaciones:
		+	<center>
	<math>		<math>
-	i	+	\left\{
		+	\begin{array}{l}
		+	a = b
		+	\\
		+	a = c
		+	\item \end{array}
		+	\right.
	</math>		</math>
-	&nbsp; que aparece en el término &nbsp;	+	</center>
		+	donde
	<math>		<math>
-	b_i	+	a
-	</math>	+	</math>,
-	, &nbsp; indica la ecuación de la que &nbsp;	+	<math>
		+	b
		+	</math>,
		+	y
	<math>		<math>
-	b_i	+	c
	</math>		</math>
-	&nbsp; es término independiente.	+	representan simplemente los miembros de estas ecuaciones ( son expresiones
		+	algebraicas ).
	<br/>		<br/>
-	El sistema anterior de &nbsp;	+	De las dos igualdades anteriores se deduce que
		+	<center>
	<math>		<math>
-	m	+	b = c
	</math>		</math>
-	&nbsp; ecuaciones lineales con &nbsp;	+	</center>
		+	Si resulta que una incognita del sistema de ecuaciones no aparece ni en
	<math>		<math>
-	n	+	a
	</math>		</math>
-	&nbsp; incognitas se puede escribir matricialmente de la siguiente forma:	+	ni en
-		+	<math>
-	<br/>	+	b
-		+	</math>,
		+	entonces la ecuación
	<center>		<center>
	<math>		<math>
-	\left(	+	b = c
-	\begin{array}[c]{cccc}	+
-	a_{11} & a_{12} & \ldots & a_{1n}	+
-	\\	+
-	a_{21} & a_{22} & \ldots & a_{2n}	+
-	\\	+
-	\vdots & \vdots & \ddots & \vdots	+
-	\\	+
-	a_{m1} & a_{m2} & \ldots & a_{mn}	+
-	\end{array}	+
-	\right)	+
-	\cdot	+
-	\left(	+
-	\begin{array}[c]{c}	+
-	x_1	+
-	\\	+
-	x_2	+
-	\\	+
-	\vdots	+
-	\\	+
-	x_n	+
-	\end{array}	+
-	\right)	+
-	\, = \,	+
-	\left(	+
-	\begin{array}[c]{c}	+
-	b_1	+
-	\\	+
-	b_2	+
-	\\	+
-	\vdots	+
-	\\	+
-	b_m	+
-	\end{array}	+
-	\right)	+
	</math>		</math>
	</center>		</center>
		+	no contendría dicha incognita.
	<br/>		<br/>
-	De izquierda a derecha, la primera matriz, en la igualdad anterior es la '''''matriz de los coeficientes''''' y la llamaremos	+	Este proceso de eliminación de incognitas se puede repetir varias veces hasta
-	&nbsp;	+	llegar a una ecuación con solo una incognita, digamos
	<math>		<math>
-	\mathbf{A}	+	x
	</math>		</math>
-	, la segunda matriz es la matriz de las incognitas y la llamaremos &nbsp;	+	.
		+
		+	<br/>
		+
		+	Una vez que se obtiene la solución de esta ecuación se sustituye
	<math>		<math>
-	\mathbf{B}	+	x
	</math>		</math>
-	. La tercera es la matriz de los terminos indedependientes y la llamaremos &nbsp;	+	por su solución en otras ecuaciones dode aparezca
	<math>		<math>
-	\mathbf{B}	+	x
	</math>		</math>
-	.	+	para reducir el número de incognitas en dichas ecuaciones.
	<br/>		<br/>
-	Con esta notación, nuestro sistema de ecuaciones lineales se puede representar de la	+	===Ejemplo===
-	siguiente manera:	+
	<br/>		<br/>
		+	El sistema de ecuaciones
	<center>		<center>
	<math>		<math>
-	\mathbf{A} \cdot \mathbf{X} \, = \, \mathbf{B}	+	\left\{
		+	\begin{array}{l}
		+	2x - 3y = -1
		+	\\
		+	2x + 4y = 6
		+	\end{array}
		+	\right.
	</math>		</math>
	</center>		</center>
		+	es equivalente a este otro
		+	<center>
		+	<math>
		+	\left\{
		+	\begin{array}{l}
		+	2x = -1 + 3y
		+	\\
		+	2x = 6 -4y
		+	\end{array}
		+	\right.
		+	</math>
		+	</center>
		+	El segundo sistema lo he obtenido pasando los terminos en
		+	<math>
		+	y
		+	</math>
		+	del miembro de la izquierda al miembro de la derecha en cada una de las
		+	ecuaciones del primer sistema.
	<br/>		<br/>
-	La matriz de los coeficientes ampliada con los terminos independientes o	+	Del segundo sistema se deduce que
-	simplemente la	+	<center>
-	'''''matriz ampliada''''' es la matriz de los coeficientes,	+
	<math>		<math>
-	\mathbf{A}	+	-1 + 3y = 6 - 4y
	</math>		</math>
-	, a la que se añade la columna de los terminos independientes, &nbsp;	+	</center>
		+	que es una ecuación con una sola incognita cuya solución es &nbsp;
	<math>		<math>
-	\mathbf{B}	+	y = 1
-	</math>	+	</math>.
-	&nbsp;:	+
	<br/>		<br/>
		+	Sustituyendo
		+	<math>
		+	y
		+	</math>
		+	por 1 en la primera ecuación del sistema de partida se tiene que
	<center>		<center>
	<math>		<math>
-	\mathbf{A}|\mathbf{B} \, = \,	+	2x - 3 = -1
-	\left(	+
-	\left.	+
-	\begin{array}[c]{cccc}	+
-	a_{11} & a_{12} & \ldots & a_{1n}	+
-	\\	+
-	a_{21} & a_{22} & \ldots & a_{2n}	+
-	\\	+
-	\vdots & \vdots & \ddots & \vdots	+
-	\\	+
-	a_{m1} & a_{m2} & \ldots & a_{mn}	+
-	\end{array}	+
-	\right|	+
-	\begin{array}[c]{c}	+
-	b_1	+
-	\\	+
-	b_2	+
-	\\	+
-	\vdots	+
-	\\	+
-	b_m	+
-	\end{array}	+
-	\right)	+
	</math>		</math>
	</center>		</center>
		+	que es una ecuación con una sola incognita y cuya solución es &nbsp;
		+	<math>
		+	x = 1
		+	</math>.
	<br/>		<br/>
-	==Solución de un sistema de ecuaciones lineales==	+	==Método de sustitución==
	<br/>		<br/>
-	Serán soluciones de un sistema de ecuaciones lineales todas las n-tuplas &nbsp;	+	Supongamos que un sistema de ecuaciones se puede poner de la forma
		+	<center>
	<math>		<math>
-	\left(	+	\left\{
-	\, s_1, \, s_2, \, \ldots, \, s_n \,	+	\begin{array}{l}
-	\right)	+	a \cdot b + c = d
		+	\\
		+	a + e = f
		+	\end{array}
		+	\right.
	</math>		</math>
-	&nbsp; tales que al sustituir &nbsp;	+	</center>
		+	Entonces podemos despejar
	<math>		<math>
-	x_i	+	a
	</math>		</math>
-	&nbsp; por &nbsp;	+	en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
		+	<center>
	<math>		<math>
-	s_i	+	\left( \, f - e \, \right) \cdot b + c = d
	</math>		</math>
-	, &nbsp; para &nbsp;	+	</center>
-	<math>	+	Lo que se busca es que esta ecuación dependa de menos incognitas que las de
-	i = 1, \, 2, \, \ldots, \, n	+	partida.
-	</math>	+
-	, &nbsp; todas las ecuaciones del sistema se conviertan en identidades.	+
	<br/>		<br/>
-	Al conjunto	+	Aqui &nbsp;
-	de todas las soluciones del sistema se le llama solución general, y a cada una de las	+	<math>
-	soluciones que forman dicho conjunto, solución particular.	+	a, \, b, \, c, \, d, \, e
		+	</math>
		+	&nbsp; y &nbsp;
		+	<math>
		+	f
		+	</math>
		+	&nbsp; son expresiones algebraicas de las incognitas del sistema.
	<br/>		<br/>
Línea 250:		Línea 333:
	<br/>		<br/>
-	La solución del sistema de ecuaciones lineales	+	Intentemos resolver
-		+
	<center>		<center>
	<math>		<math>
-	\left\{	+	\left\{
	\begin{array}{l}		\begin{array}{l}
-	5x + 2y = 9	+	4x + 3y = 7
	\\		\\
-	4x - 3y = -2	+	2x - y = 1
	\end{array}		\end{array}
	\right.		\right.
	</math>		</math>
	</center>		</center>
-		+	La primera ecuación se puede reescribir de la forma
-	<br/>	+
-		+
-	es	+
	<center>		<center>
	<math>		<math>
-	\left( \,	+	2 \cdot \left( \, 2x \, \right) + 3y = 7
-	\begin{array}{c}	+
-	x	+
-	\\	+
-	y	+
-	\end{array}	+
-	\, \right)	+
-	=	+
-	\left( \,	+
-	\begin{array}{c}	+
-	1	+
-	\\	+
-	2	+
-	\end{array}	+
-	\, \right)	+
	</math>		</math>
	</center>		</center>
-		+	Por otra parte, de la segunda ecuación del sistema se deduce que
-	porque cuando sustituimos	+	<center>
	<math>		<math>
-	x	+	2x = 1 + y
	</math>		</math>
-	por 1 e	+	</center>
		+	Sustituyendo &nbsp;
	<math>		<math>
-	y	+	2x
	</math>		</math>
-	por 2 en el sistema de ecuaciones, obtenemos	+	&nbsp; por
		+	<math>
		+	1 + y
		+	</math>
		+	en
	<center>		<center>
	<math>		<math>
-	\left\{	+	2 \cdot \left( \, 2x \, \right) + 3y = 7
-	\begin{array}{l}	+
-	5 \cdot 1 + 2 \cdot 2 = 9	+
-	\\	+
-	4 \cdot 1 - 3 \cdot 2 = -2	+
-	\end{array}	+
-	\right.	+
	</math>		</math>
	</center>		</center>
-	que son identidades ( igualdades ciertas ).	+	se tiene que
-		+	<center>
-	<br/>	+	<math>
-		+	2 \cdot \left( \, 1 + y \, \right)+ 3y = 7
-	==Tipos de sistemas de ecuaciones lineales==	+	</math>
		+	</center>
		+	que es una ecuación con solo una incognita y cuya solución es
		+	<math>
		+	y = 1
		+	</math>.
	<br/>		<br/>
		+	Sustituyendo
		+	<math>
		+	y
		+	</math>
		+	por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos
		+	una ecuación de una sola incognita
	<center>		<center>
	<math>		<math>
-	\left\{	+	4 + 3y = 7
-	\begin{array}{l}	+
-	COMPATIBLES	+
-	\left\{	+
-	\begin{array}{l}	+
-	DETERMINADOS	+
-	\\	+
-	INDETERMINADOS	+
-	\end{array}	+
-	\right.	+
-	\\	+
-	INCOMPATIBLES	+
-	\end{array}	+
-	\right.	+
	</math>		</math>
	</center>		</center>
		+	cuya solución es &nbsp;
		+	<math>
		+	x = 1
		+	</math>.
		+	<br/>
		+	==Método de Gauss==
	<br/>		<br/>
-	===Sistemas de ecuaciones compatibles e incompatibles===	+	[[Imagen:gauss.jpg|frame|Gauss es uno de los matematicos mas
		+	importantes de todos los tiempos. ¡Fue un GENIO!]]
	<br/>		<br/>
-	Un sistema de ecuaciones lineales es '''''compatible''''' cuando tiene al menos una	+	El método de Gauss consiste en transformar el sistema dado en otro equivalente.
-	solución e '''''incompatible''''' cuando NO tiene ninguna solución.	+	Para ello tomamos la [[Definición y tipos|matriz ampliada]] del
		+	sistema y mediante las [[Matriz inversa#Operaciones elementales por filas en una matriz|operaciones elementales]]
		+	por filas la transformamos en una matriz triangular superior ( o
		+	inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil
		+	de resolver.
	<br/>		<br/>
-	====Ejemplo====	+	Es esencialmente el [[Métodos de resolución de sistemas de ecuaciones lineales#método de reducción|método de reducción]]. En el método de Gauss se
		+	opera con ecuaciones, como se hace en el método de reducción, pero uno se ahorra
		+	el escribir las incognitas porque al ir los coeficientes de una misma incognita
		+	siempre en una misma columna, uno sabe en todo momento cual es la incognita a la
		+	que multiplican.
	<br/>		<br/>
-	Un sistema de ecuaciones lineales incompatible es	+	===Ejemplo===
		+
		+	<br/>
		+
		+	La matriz ampliada del sistema de ecuaciones:
		+
		+	<br/>
	<center>		<center>
	<math>		<math>
	\left\{		\left\{
-	\begin{array}{l}	+	\begin{array}[c]{ccc}
-	2x = 4	+	x \, + \, y \, + \, z & = & ~~3
-	\\	+	\\
-	3x = 3	+	x \, + \, y \, - \, z & = & ~~1
-	\end{array}	+	\\
		+	x \, - \, y \, - \, z & = & -1
		+	\end{array}
	\right.		\right.
	</math>		</math>
Línea 367:		Línea 452:
	<br/>		<br/>
-	ya que de la primera ecuación se deduce que &nbsp;	+	es:
-	<math>	+
-	x = 2	+
-	</math>	+
-	&nbsp; mientras que de la segunda se deduce que &nbsp;	+
-	<math>	+
-	x = 1	+
-	</math>	+
	<br/>		<br/>
-	Como es imposible que
-	<math>
-	x
-	</math>
-	sea dos y uno al mismo tiempo, ambas igualdades
	<center>		<center>
	<math>		<math>
-	x = 1 \qquad \text{y} \qquad x = 2	+	\left(
		+	\left.
		+	\begin{array}[c]{ccc}
		+	~~1 & ~~1 & ~~1
		+	\\
		+	~~1 & ~~1 & -1
		+	\\
		+	~~1 & -1 & -1
		+	\end{array}
		+	\right|
		+	\begin{array}[c]{c}
		+	~~3
		+	\\
		+	~~1
		+	\\
		+	-1
		+	\end{array}
		+	\right)
	</math>		</math>
	</center>		</center>
-	son incompatibles y por eso el sistema de ecuaciones con el que iniciabamos este
-	ejemplo no tiene solución.
	<br/>		<br/>
-	====Teorema de Rouche-Fröbenius====	+	Si a la tercera y segunda fila le restamos la primera, obtenemos:
	<br/>		<br/>
-	[[Imagen:frobenius.jpg|frame|Georg F. Fröbenius fue un matematico aleman que nacio en	+	<center>
-	1849 y murio en 1917. ¡Gracias Georg por tu legado!]]	+
-		+
-	<br/>	+
-		+
-	Un sistema de &nbsp;	+
	<math>		<math>
-	m	+	\left(
		+	\left.
		+	\begin{array}[c]{ccc}
		+	~~1 & ~~1 & ~~1
		+	\\
		+	~~0 & ~~0 & -2
		+	\\
		+	~~0 & -2 & -2
		+	\end{array}
		+	\right|
		+	\begin{array}[c]{c}
		+	~~3
		+	\\
		+	-2
		+	\\
		+	-4
		+	\end{array}
		+	\right)
	</math>		</math>
-	&nbsp; ecuaciones lineales con &nbsp;	+	</center>
-	<math>	+
-	n	+
-	</math>	+
-	&nbsp; incognitas es compatible ( tiene solución ) si, y sólo si, el [[Rango de una matriz|rango]] de la matriz de los coeficientes coincide con el rango de la matriz	+
-	ampliada.	+
	<br/>		<br/>
-	====Ejemplo:sistemas homogeneos====	+	Lo que acabamos de hacer es equivalente a restar a la tercera y segunda
		+	ecuación la primera.
	<br/>		<br/>
-	Un sistema de ecuaciones es '''''homogéneo''''' cuando todos sus terminos independientes	+	Si ahora intercambiamos la segunda y tercera filas ( ecuaciones ), obtenemos
-	son cero.	+
	<br/>		<br/>
-	En un sistema de ecuaciones homogeneo, la matriz &nbsp;	+	<center>
	<math>		<math>
-	\mathbf{B}	+	\left(
		+	\left.
		+	\begin{array}[c]{ccc}
		+	~~1 & ~~1 & ~~1
		+	\\
		+	~~0 & -2 & -2
		+	\\
		+	~~0 & ~~0 & -2
		+	\end{array}
		+	\right|
		+	\begin{array}[c]{c}
		+	~~3
		+	\\
		+	-4
		+	\\
		+	-2
		+	\end{array}
		+	\right)
	</math>		</math>
-	&nbsp; de los terminos independientes es una matriz nula, de manera que el	+	</center>
-	[[Rango de una matriz|rango]] de la	+
-	matriz de los coeficientes y el de la	+
-	matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius,	+
-	que un sistema homogeneo SIEMPRE es compatible.	+
	<br/>		<br/>
-	En cualquier sistema homogeneo, una solución particular es la solución trivial (	+	que es la matriz ampliada del sistema de ecuaciones:
-	todas las incognitas son cero ).	+
	<br/>		<br/>
-	===Sistemas de ecuaciones lineales compatibles determinados===	+	<center>
		+	<math>
		+	\left\{
		+	\begin{array}[c]{rcl}
		+	x \, + \, y \, + \, z & = & ~~3
		+	\\
		+	-2y \, - \, 2z & = & -4
		+	\\
		+	-2z & = & -2
		+	\end{array}
		+	\right.
		+	</math>
		+	</center>
	<br/>		<br/>
-	Un sistema de ecuaciones lineales es '''''compatible determinado''''' cuando tiene	+	que es equivalente al inicial.
-	solución única.	+
	<br/>		<br/>
-	====Ejemplo====	+	Solucionamos la tercera ocuacion para obtener &nbsp;
		+	<math>
		+	z
		+	</math>
		+	&nbsp;:
	<br/>		<br/>
-	El sistema de ecuaciones lineales	+	<center>
		+	<math>
		+	z \, = \, 1
		+	</math>
		+	</center>
		+
		+	<br/>
		+	En la primera y segunda ecuación, sustituimos &nbsp;
		+	<math>
		+	z
		+	</math>
		+	&nbsp; por la solucion de la tercera ecuación &nbsp; ( &nbsp;
		+	<math>
		+	1 \to z
		+	</math>
		+	&nbsp; ), para obtener:
	<br/>		<br/>
Línea 460:		Línea 597:
	<center>		<center>
	<math>		<math>
-	\left\{	+	\left\{
-	\begin{array}{l}	+	\begin{array}[c]{rcl}
-	4x + 3y = 7	+	x \, + \, y \, + \, 1 & = & ~~3
-	\\	+	\\
-	2x - y = 1	+	-2y \, - \, 2 & = & -4
-	\end{array}	+	\end{array}
	\right.		\right.
	</math>		</math>
Línea 472:		Línea 609:
	<br/>		<br/>
-	tiene una única solución	+	La segunda ecuación es ahora una ecuación con una sola incognita, &nbsp;
		+	<math>
		+	y
		+	</math>
		+	, que resolvemos para obtener &nbsp;
		+	<math>
		+	y \, = \, 1
		+	</math>
		+	. &nbsp; Sustituimos, en la primera ecuación, &nbsp;
		+	<math>
		+	y
		+	</math>
		+	&nbsp; por 1 &nbsp; ( &nbsp;
		+	<math>
		+	1 \to y
		+	</math>
		+	&nbsp; ). Esto nos da una ecuación en &nbsp;
		+	<math>
		+	x
		+	</math>
		+	&nbsp;:
		+
		+	<br/>
		+
	<center>		<center>
	<math>		<math>
-	\left( \,	+	x \, + \, 1 \, + \, 1 \, = \, 3
-	\begin{array}{c}	+
-	x	+
-	\\	+
-	y	+
-	\end{array}	+
-	\, \right)	+
-	=	+
-	\left( \,	+
-	\begin{array}{c}	+
-	1	+
-	\\	+
-	1	+
-	\end{array}	+
-	\, \right)	+
	</math>		</math>
	</center>		</center>
-
-	y se trata, por tanto, de un sistema de ecuaciones compatible determinado.
	<br/>		<br/>
-	===Sistemas de ecuaciones lineales compatibles indeterminados===	+	que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
	<br/>		<br/>
-	Un sistema de ecuaciones lineales es '''''compatible indeterminado''''' cuando tiene infinitas	+	<center>
-	soluciones.	+	<math>
		+	x \, = \, y \, = \, z \, = \, 1
		+	</math>
		+	</center>
	<br/>		<br/>
-	Un sistema de ecuaciones lineales es '''''compatible indeterminado''''' si y	+	==Método de la matriz inversa==
-	solo si tiene mas de una solución, es decir:	+
-	Si un sistema de ecuaciones lineales tiene mas de una solución, entonces tiene infinitas soluciones.	+	Un sistema de ecuaciones lineales se puede escribir en [[Definición y tipos#Definición|forma matricial]]:
-		+
-	Cuando el sistema de ecuaciones lineales es compatible indeterminado hay que	+
-	distinguir entre la solución general del sistema de ecuaciones y las soluciones	+
-	particulares del mismo.	+
	<br/>		<br/>
-	Cuando se da la solución de un sistema de ecuaciones lineales compatible	+	<center>
-	indeterminado lo que se da es un la solución general. Esta solución depende de	+	<math>
-	uno o mas parametros.	+	\mathbf{A} \cdot \mathbf{X} \, = \, \mathbf{B}
		+	</math>
		+	</center>
	<br/>		<br/>
-	Dando a los parametros unos valores determinados obtenemos una solución	+	Si &nbsp;
-	particular del sistema; dando a los parametros otros valores distintos obtenemos	+	<math>
-	otra solución particular del sistema.	+	\mathbf{A}^{-1}
		+	</math>
		+	&nbsp; existe, es decir, si &nbsp;
		+	<math>
		+	\mathbf{A}
		+	</math>
		+	&nbsp; es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
		+	la igualdad anterior por la izquierda por &nbsp;
		+	<math>
		+	\mathbf{A}^{-1}
		+	</math>
		+	, para obtener:
	<br/>		<br/>
-	El número de parametros en la solución general coincide con el número de	+	<center>
-	incognitas menos el rango de la matriz de los coeficientes del sistema.	+	<math>
		+	\mathbf{X} \, = \, \mathbf{A}^{-1} \cdot \mathbf{B}
		+	</math>
		+	</center>
	<br/>		<br/>
-	Si el sistema es compatible, existen dos posibilidades:	+	que es la solución del sistema de ecuaciones lineales de matriz de coeficientes &nbsp;
		+	<math>
		+	\mathbf{A}
		+	</math>
		+	&nbsp; y matriz de terminos independientes &nbsp;
		+	<math>
		+	\mathbf{B}
		+	</math>
		+	.
	<br/>		<br/>
-	1. Que el rango de la matriz de los coeficientes sea menor que el número de incognitas.	+	==Regla de Cramer==
	<br/>		<br/>
-	2. Que el rango de la matriz de los coeficientes sea igual al número de incognitas.	+	[[Imagen:cramer2.gif|frame|Gabriel Cramer nacio Ginebra ( Suiza ) 1704 y murio en 1752. A
		+	él le debemos la regla que lleva su nombre. ¡Gracias Gabriel por tu contribución a las Matemáticas!]]
	<br/>		<br/>
-	En el primer caso el sistema es compatible	+	Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede
-	indeterminado y en el segundo caso el sistema es	+	utilizar cuando la matriz &nbsp;
-	[[Definición y tipos#Sistemas de ecuaciones lineales compatibles determinados|compatible determinado]].	+	<math>
		+	\mathbf{A}
		+	</math>
		+	&nbsp; de coeficientes del sistema es cuadrada y de determinante no nulo. El que &nbsp;
		+	<math>
		+	\mathbf{A}
		+	</math>
		+	&nbsp; sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
		+	coincide.
	<br/>		<br/>
-	====Ejemplo====	+	Cuando el sistema de ecuaciones
-		+
-	<br/>	+
-		+
-	El sistema de ecuaciones	+
	<br/>		<br/>
Línea 562:		Línea 733:
	<center>		<center>
	<math>		<math>
-	\left\{	+	\left.
-	\begin{array}{l}	+	\begin{array}{c}
-	4x + 3y = 0	+	a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1
-	\\	+	\\
-	2x - y = 0	+	a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2
-	\end{array}	+	\\
-	\right.	+	\dotfill
		+	\\
		+	a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m
		+	\end{array}
		+	\right\}
	</math>		</math>
	</center>		</center>
Línea 574:		Línea 749:
	<br/>		<br/>
-	es homogeneo.	+	satisface las condiciones arriba mencionadas, su solución viene dada por:
	<br/>		<br/>
-	Como el determinante de la matriz de los coeficientes
	<center>		<center>
	<math>		<math>
-	\left|	+	x_1 \, = \, \frac
-	\begin{array}[c]{cc}	+	{
-	4 & 3	+	\left|
		+	\begin{array}[c]{cccc}
		+	b_1 & a_{12} & \ldots & a_{1n}
	\\		\\
-	2 & -1	+	b_2 & a_{22} & \ldots & a_{2n}
		+	\\
		+	\vdots & \vdots & \ddots & \vdots
		+	\\
		+	b_m & a_{m2} & \ldots & a_{mn}
	\end{array}		\end{array}
	\right|		\right|
		+	}
		+	{|\mathbf{A}|}
		+	, \qquad \qquad x_2 \, = \, \frac
		+	{
		+	\left|
		+	\begin{array}[c]{cccc}
		+	a_{11} & b_1 & \ldots & a_{1n}
		+	\\
		+	a_{21} & b_2 & \ldots & a_{2n}
		+	\\
		+	\vdots & \vdots & \ddots & \vdots
		+	\\
		+	a_{m1} & b_m & \ldots & a_{mn}
		+	\end{array}
		+	\right|
		+	}
		+	{|\mathbf{A}|}, \qquad \qquad \ldots \ldots
	</math>		</math>
	</center>		</center>
-	es distinto de cero &nbsp;	+
-	<math>	+	<br/>
-	\left( \, 4 \cdot \left( \, -1 \, \right) - 2 \cdot 3 = -10 \, \right)	+
-	</math>,	+
-	&nbsp; el rango de	+
-	<math>	+
-	\mathbf{A}	+
-	</math>	+
-	coincide con el número de incognitas ( 3 ) y, por lo tanto, el	+
-	sistema es [[Tipos de sistemas de ecuaciones lineales#Sistemas compatibles determinados|compatible determinado]], es decir tiene una solución única.	+
	<center>		<center>
	<math>		<math>
-	\left( \,	+	\ldots \ldots, \qquad \qquad x_n \, = \, \frac
-	\begin{array}{c}	+	{
-	x	+	\left|
-	\\	+	\begin{array}[c]{cccc}
-	y	+	a_{11} & a_{12} & \ldots & b_1
-	\end{array}	+	\\
-	\, \right)	+	a_{21} & a_{22} & \ldots & b_2
-	=	+	\\
-	\left( \,	+	\vdots & \vdots & \ddots & \vdots
-	\begin{array}{c}	+	\\
-	0	+	a_{m1} & a_{m2} & \ldots & b_m
-	\\	+	\end{array}
-	0	+	\right|
-	\end{array}	+	}
-	\, \right)	+	{|\mathbf{A}|}
		+	\qquad \qquad
	</math>		</math>
	</center>		</center>
Línea 623:		Línea 813:
	<br/>		<br/>
-	====Ejemplo====	+	En general
	<br/>		<br/>
-	El sistema de ecuaciones
	<center>		<center>
	<math>		<math>
-	x + y = 2	+	x_i \, = \, \frac{|\mathbf{A}_i|}{|\mathbf{A}|}
	</math>		</math>
	</center>		</center>
-	esta formado por una única ecuación y es compatible indeterminado, ya que
-	tiene mas de dos soluciones.
	<br/>		<br/>
-	<center>	+	donde &nbsp;
	<math>		<math>
-	\left( \,	+	\mathbf{A}_i
-	\begin{array}{c}	+
-	x	+
-	\\	+
-	y	+
-	\end{array}	+
-	\, \right)	+
-	=	+
-	\left( \,	+
-	\begin{array}{c}	+
-	1	+
-	\\	+
-	1	+
-	\end{array}	+
-	\, \right)	+
	</math>		</math>
-	</center>	+	&nbsp; es la matriz que se obtiene sustituyendo la i-esima columna de &nbsp;
-	e	+
-	<center>	+
	<math>		<math>
-	\left( \,	+	\mathbf{A}
-	\begin{array}{c}	+	</math>
-	x	+	&nbsp; por la [[Definición y tipos|matriz de los terminos independientes]], &nbsp;
-	\\	+	<math>
-	y	+	B
-	\end{array}	+
-	\, \right)	+
-	=	+
-	\left( \,	+
-	\begin{array}{c}	+
-	2	+
-	\\	+
-	0	+
-	\end{array}	+
-	\, \right)	+
	</math>		</math>
-	</center>	+	&nbsp;.
	<br/>		<br/>
-	Para dar la solución de esta ecuación tenemos que introducir un parametro que	+	===Ejemplo===
-	podemos llamar	+
-	<math>	+
-	t	+
-	</math>.	+
	<br/>		<br/>
-		+	Consideremos el sistema de ecuaciones:
-	La solución general, en este caso, esta parametrizada por un solo parametro	+
-	porque	+
-		+
-	<center>	+
-	número de incognitas ( 2 ) - rango de la matriz de los coeficientes( 1 ) = 1	+
-	</center>	+
	<br/>		<br/>
-	La matriz de los coeficientes es una matriz con una fila y dos columnas
	<center>		<center>
	<math>		<math>
-	\mathbf{A} = \left( \, 1 \qquad 1 \, \right)	+	\left\{
		+	\begin{array}[c]{rcl}
		+	x \, + \, y \, = \, 2
		+	\\
		+	x \, - \, y \, = \, 0
		+	\end{array}
		+	\right.
	</math>		</math>
	</center>		</center>
-	cuyo rango es 1 ( la unica manera posible de que una matriz tenga rango menor que 1 es teniendo todos sus elementos cero, en cuyo
-	caso tendria rango cero ).
	<br/>		<br/>
-	Si hacemos &nbsp;	+	En este sistema de ecuaciones lineales, la matriz &nbsp;
	<math>		<math>
-	y = t	+	\mathbf{A}
	</math>		</math>
-	&nbsp; nos queda que	+	&nbsp; de los coeficientes es una matriz cuadrada y &nbsp;
-	<center>	+
	<math>		<math>
-	x = 1 - t	+	|\mathbf{A}| \, = \,
		+	\left|
		+	\begin{array}[c]{cc}
		+	1 & ~~1
		+	\\
		+	1 & -1
		+	\end{array}
		+	\right|
		+	\, = \, -2 \neq 0
	</math>		</math>
-	</center>	+	. Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
-	de manera que la solución general seria	+
	<br/>		<br/>
Línea 724:		Línea 884:
	<center>		<center>
	<math>		<math>
-	\left( \,	+	x \, = \, \frac
-	\begin{array}{c}	+	{
-	x	+	\left|
-	\\	+	\begin{array}[c]{cc}
-	y	+	2 & ~~1
-	\end{array}	+	\\
-	\, \right)	+	0 & -1
-	=	+	\end{array}
-	\left( \,	+	\right|
-	\begin{array}{c}	+	}
-	1 - t	+	{|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1
-	\\	+	\qquad \qquad y \, = \, \frac
-	t	+	{
-	\end{array}	+	\left|
-	\, \right)	+	\begin{array}[c]{cc}
-	=	+	1 & 2
-	\left( \,	+	\\
-	\begin{array}{c}	+	1 & 0
-	1	+	\end{array}
-	\\	+	\right|
-	0	+	}
-	\end{array}	+	{|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1
-	\, \right)	+
-	+	+
-	t \cdot \left( \,	+
-	\begin{array}{c}	+
-	-1	+
-	\\	+
-	~1	+
-	\end{array}	+
-	\, \right)	+
	</math>		</math>
	</center>		</center>

---

Revisión de 16:39 27 sep 2010

Tabla de contenidos 1 Introducción 2 Método de reducción 2.1 Ejemplo 3 Método de igualación 3.1 Ejemplo 4 Método de sustitución 4.1 Ejemplo 5 Método de Gauss 5.1 Ejemplo 6 Método de la matriz inversa 7 Regla de Cramer 7.1 Ejemplo

Introducción

Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones.

Los métodos de igualación, sustitución y reducción consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas facil, ¿no?).

A estas ecuaciones, con solo una incognita, se llega a traves de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas.

Así, es posible que en uno de estos pasos de eliminación de incognitas se utilize un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se utilize otro método ( el de igualación, por ejemplo ).

Cada vez que se encuentra la solución para una incognita, se sustituye esta incognita por su solución para obtener asi ecuaciones con menos incognitas.

Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar para resolver sistemas de ecuaciones compatibles determinados e indeterminados.

Estos mismos métodos tambien pueden utilizarse para comprobar si un sistema de ecuaciones es compatible o no. La utilizacion de cualquiera de ellos conduciria, en el caso de que el sistema fuese incompatible, a una igualdad que es falsa, por ejemplo:

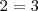
El método de la matriz inversa y la regla de Cramer solo se pueden utilizar en el caso de que el sistema de ecuaciones lineales sea compatible determinado.

Método de reducción

Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número de incognitas hasta llegar a ecuaciones con solo una incognita.

Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de la ecuación por dicho número.

Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho ( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las ecuaciones que se suman.

Ejemplo

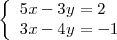
Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones

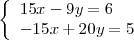
El sumar ambas ecuaciones nos da la ecuación

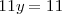
que es una ecuación con una sola incognita y cuya solución es

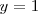
La elección de los factores 3 y -5 se ha hecho precisamente para que la desaparezca al sumar ambas ecuaciones.

Sutituyendo 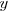por uno en la primera ecuación del sistema de ecuaciones de partida, se obtiene

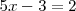
que es otra ecuación con una sola incognita y cuya solución es   .

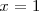Método de igualación

El método de igualación consiste en lo siguiente:

Supongamos que tenemos dos ecuaciones:

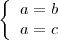
donde , , 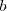y representan simplemente los miembros de estas ecuaciones ( son expresiones algebraicas ).

De las dos igualdades anteriores se deduce que

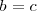
Si resulta que una incognita del sistema de ecuaciones no aparece ni en ni en 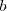, entonces la ecuación

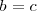
no contendría dicha incognita.

Este proceso de eliminación de incognitas se puede repetir varias veces hasta llegar a una ecuación con solo una incognita, digamos .

Una vez que se obtiene la solución de esta ecuación se sustituye por su solución en otras ecuaciones dode aparezca para reducir el número de incognitas en dichas ecuaciones.

Ejemplo

El sistema de ecuaciones

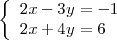
es equivalente a este otro

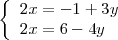
El segundo sistema lo he obtenido pasando los terminos en del miembro de la izquierda al miembro de la derecha en cada una de las ecuaciones del primer sistema.

Del segundo sistema se deduce que

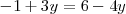
que es una ecuación con una sola incognita cuya solución es   .

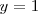Sustituyendo por 1 en la primera ecuación del sistema de partida se tiene que

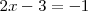
que es una ecuación con una sola incognita y cuya solución es   .

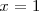Método de sustitución

Supongamos que un sistema de ecuaciones se puede poner de la forma

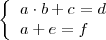
Entonces podemos despejar en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:

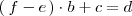
Lo que se busca es que esta ecuación dependa de menos incognitas que las de partida.

Aqui 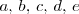    y 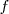    son expresiones algebraicas de las incognitas del sistema.

Ejemplo

Intentemos resolver

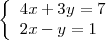
La primera ecuación se puede reescribir de la forma

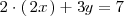
Por otra parte, de la segunda ecuación del sistema se deduce que

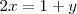
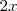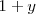Sustituyendo     por en

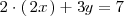
se tiene que

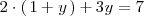
que es una ecuación con solo una incognita y cuya solución es .

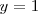Sustituyendo por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos una ecuación de una sola incognita

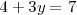
cuya solución es   .

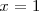Método de Gauss

El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales por filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.

Es esencialmente el método de reducción. En el método de Gauss se opera con ecuaciones, como se hace en el método de reducción, pero uno se ahorra el escribir las incognitas porque al ir los coeficientes de una misma incognita siempre en una misma columna, uno sabe en todo momento cual es la incognita a la que multiplican.

Ejemplo

La matriz ampliada del sistema de ecuaciones:

es:

Si a la tercera y segunda fila le restamos la primera, obtenemos:

Lo que acabamos de hacer es equivalente a restar a la tercera y segunda ecuación la primera.

Si ahora intercambiamos la segunda y tercera filas ( ecuaciones ), obtenemos

que es la matriz ampliada del sistema de ecuaciones:

que es equivalente al inicial.

Solucionamos la tercera ocuacion para obtener    :

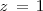
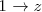En la primera y segunda ecuación, sustituimos     por la solucion de la tercera ecuación   (     ), para obtener:

La segunda ecuación es ahora una ecuación con una sola incognita,   , que resolvemos para obtener 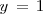  .   Sustituimos, en la primera ecuación,     por 1  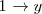 (     ). Esto nos da una ecuación en    :

que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:

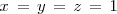
Método de la matriz inversa

Un sistema de ecuaciones lineales se puede escribir en forma matricial:

Si 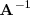    existe, es decir, si 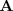    es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda la igualdad anterior por la izquierda por 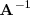  , para obtener:

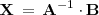
que es la solución del sistema de ecuaciones lineales de matriz de coeficientes 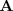    y matriz de terminos independientes   .

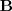Regla de Cramer

Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede utilizar cuando la matriz 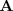    de coeficientes del sistema es cuadrada y de determinante no nulo. El que 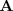    sea cuadrada significa que el numero de incognitas y el numero de ecuaciones coincide.

Cuando el sistema de ecuaciones

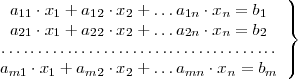
satisface las condiciones arriba mencionadas, su solución viene dada por:

En general

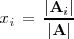
donde 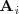    es la matriz que se obtiene sustituyendo la i-esima columna de 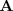    por la matriz de los terminos independientes,    .

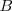Ejemplo

Consideremos el sistema de ecuaciones:

En este sistema de ecuaciones lineales, la matriz 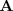    de los coeficientes es una matriz cuadrada y   . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:

   Tweet