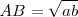El teorema de Euclides
De Wikillerato
Ya vimos el teorema de Euclides, considerando su enunciados como teoremas de la altura y del cateto, en el capítulo de triángulos y realizamos sus demostraciones gráficas.
Ahora vamos a ver su relación con la tercera proporcional. Si consideramos que:
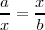
vemos que el término intermedio, x, es media proporcional entre a y b, pues:
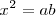
Las construcciones de la media proporcional de dos segmentos, basadas directamente en Euclides, tienen muchas aplicaciones en la resolución de problemas gráficos.
Aplicando el teorema de la altura
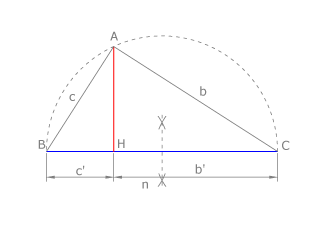
Dibujamos el segmento BC= a+b, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. Por el extremo común de los segmentos, H, dibujamos la perpendicular a BC que corta al arco en A. AH es la altura de ABC y es media proporcional de los segmentos en que divide a la hipotenusa: a y b, como ya vimos en el capítulo 2.
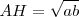
Aplicando el teorema del cateto
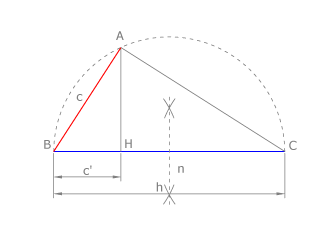
Dibujamos el segmento BC=b y BH=a, superpuestos, como vemos en la figura. Trazamos la semicircunferencia de diámetro BC. La perpendicular a BC desde H corta al arco en A.
El cateto AB es media proporcional su proyección sobre la hipotenusa, a , y de la hipotenusa, b, como ya vimos en el capítulo 2.