Arco capaz
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | + | ===Trazado del arco capaz=== | |
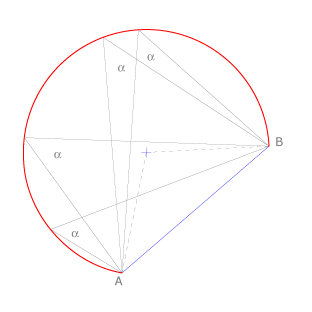
| - | + | Vamos a realizar dos trazados del arco capaz del ángulo <math>\alpha</math> para un segmento <math>AB \ </math>. | |
| - | + | [[Imagen:DibujoTecnico I-1 47.gif]] | |
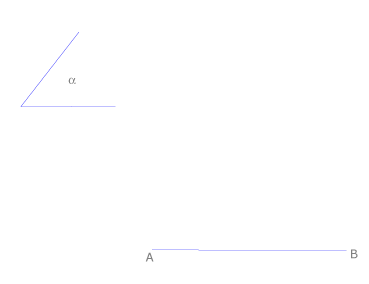
| - | + | Consideramos los siguientes datos: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[ | + | [[Imagen:DibujoTecnico I-1 48.gif]] |
| + | |||
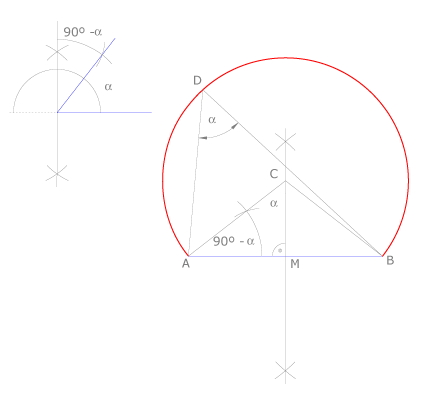
| + | '''Trazado I:''' | ||
| + | |||
| + | Dibujamos la mediatriz del segmento <math>AB \ </math>, pues el centro del arco estará sobre ella, al ser equidistante de <math>A</math> y de <math>B</math>. | ||
| + | |||
| + | Dibujamos el ángulo <math>90^\circ - \alpha</math> ,complementario del dado, con vértice en <math>A</math>. El lado de este ángulo cortará a la mediatriz en el punto <math>C</math>, centro del arco buscado. | ||
| + | |||
| + | Comprobamos que el ángulo central que abarca el arco <math>AB \ </math> mide <math> \ 2 \alpha</math>, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán <math>\alpha</math>. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 49.gif]] | ||
| + | |||
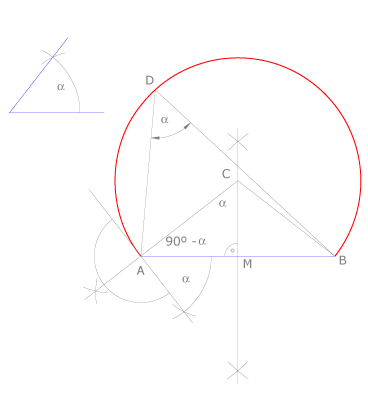
| + | '''Trazado II:''' | ||
| + | |||
| + | Dibujamos la mediatriz del segmento <math>AB \ </math>, pues el centro del arco estará sobre ella, al ser equidistante de <math>A</math> y de <math>B</math>. | ||
| + | |||
| + | Dibujamos el ángulo <math>\alpha</math> con vértice en <math>A</math>, como se ve en la figura. Trazamos por <math>A</math> la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto <math>C</math>, centro del arco buscado. | ||
| + | |||
| + | Comprobamos que el ángulo central que abarca el arco <math>AB \ </math> mide <math> \ 2 \alpha</math>, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán <math>\alpha</math>. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-1 50.gif]] | ||
Revisión de 15:51 25 sep 2008
Trazado del arco capaz
Vamos a realizar dos trazados del arco capaz del ángulo 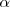 para un segmento
para un segmento 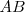 .
.
Consideramos los siguientes datos:
Trazado I:
Dibujamos la mediatriz del segmento 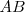 , pues el centro del arco estará sobre ella, al ser equidistante de
, pues el centro del arco estará sobre ella, al ser equidistante de 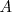 y de
y de 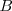 .
.
Dibujamos el ángulo 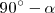 ,complementario del dado, con vértice en
,complementario del dado, con vértice en 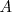 . El lado de este ángulo cortará a la mediatriz en el punto
. El lado de este ángulo cortará a la mediatriz en el punto 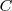 , centro del arco buscado.
, centro del arco buscado.
Comprobamos que el ángulo central que abarca el arco 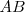 mide
mide 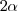 , lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán
, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán 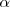 .
.
Trazado II:
Dibujamos la mediatriz del segmento 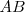 , pues el centro del arco estará sobre ella, al ser equidistante de
, pues el centro del arco estará sobre ella, al ser equidistante de 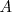 y de
y de 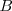 .
.
Dibujamos el ángulo 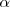 con vértice en
con vértice en 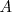 , como se ve en la figura. Trazamos por
, como se ve en la figura. Trazamos por 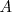 la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto
la perpendicular al lado de dicho ángulo, que cortará a la mediatriz en el punto 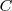 , centro del arco buscado.
, centro del arco buscado.
Comprobamos que el ángulo central que abarca el arco 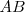 mide
mide 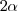 , lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán
, lo que indica que todos los ángulos inscritos que abarquen el mismo arco medirán 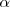 .
.