Lógica de clases
De Wikillerato
(→Leyes de Morgan) |
(→Leyes de Morgan) |
||
| Línea 177: | Línea 177: | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
| - | <td align="center"><math>\notin \, \ | + | <td align="center"><math>\notin \, \notin</math></td> |
<td align="center"><math>\notin</math></td> | <td align="center"><math>\notin</math></td> | ||
<td align="center"><math>\notin</math></td> | <td align="center"><math>\notin</math></td> | ||
Revisión de 09:55 17 abr 2007
Tabla de contenidos |
Clases
Se entiende por clase una pluralidad o conjunto de individuos que tienen una misma propiedad o propiedades. Según el diagrama de la introducción a la lógica, en la lógica proposicional, hemos estudiado las oraciones o juicios, las proposiciones y los razonamientos. En la lógica de clases, nos ocupamos de los conceptos que designan un grupo de objetos con las mismas propiedades o características. Estos grupos de objetos, son las clases.
En el lenguaje formal las clases se representan con letras mayúsculas empezando por la 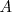 .
.
Elementos de una clase
Cada uno de los objetos integrantes de una clase, es un elemento o miembro de la clase. La relación existente entre un elemento y la clase de la que es miembro, se llama relación de pertenencia, el elemento pertenece a la clase, se simboliza: [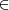 ]; este símbolo deriva de la palabra griega estí, que significa es. Por ejemplo Madrid pertenece a las capitales europeas.
]; este símbolo deriva de la palabra griega estí, que significa es. Por ejemplo Madrid pertenece a las capitales europeas. 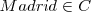 .
.
En general 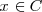 , quiere decir que
, quiere decir que  es un elemento de
es un elemento de 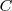 . Cuando quiero expresar que un elemento no pertenece a una clase, utilizo el símbolo:
. Cuando quiero expresar que un elemento no pertenece a una clase, utilizo el símbolo: 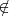 . Por ejemplo México
. Por ejemplo México 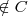 , quiere decir que México no pertenece a las capitales europeas.
, quiere decir que México no pertenece a las capitales europeas.
Las clases se pueden definir por extensión y comprensión. Por extensión enumerando sus elementos; por comprensión expresando sus propiedades comunes.
La comprensión expresa su definición en términos de idea o concepto, es decir el significado de la clase o del concepto. La extensión hace referencia a sus elementos o bien de forma total:  o bien de forma parcial:
o bien de forma parcial: 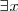 .
.
Relaciones entre clases
1. Si todos los elementos de 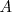 son también de
son también de 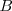 , las clases son idénticas o iguales:
, las clases son idénticas o iguales: 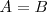 .
.
2. En el caso de que ningún elemento de 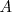 sea elemento de
sea elemento de 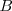 y viceversa, las clases son disjuntas: Por ejemplo la clase de los madrileños y la de los sevillanos:
y viceversa, las clases son disjuntas: Por ejemplo la clase de los madrileños y la de los sevillanos:  .
.
3. Si ambas clases tienen al menos un elemento en común, se expresa así: 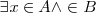 y también
y también 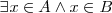 . El signo
. El signo  se llama cuantificador universal, quiere decir que hay al menos un elemento.
se llama cuantificador universal, quiere decir que hay al menos un elemento.
4. Todos los elementos de la clase 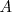 son también de la clase
son también de la clase 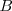 ,
Pero no a la inversa.
,
Pero no a la inversa. 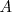 es una subclase de
es una subclase de 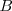 o está incluida en
o está incluida en 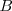 .
.
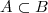 . Por ejemplo: Los alumnos de primero de la Educación Secundaria Obligatoria y los alumnos de todo el Colegio.
. Por ejemplo: Los alumnos de primero de la Educación Secundaria Obligatoria y los alumnos de todo el Colegio.
5. Clase unitaria es la que sólo tiene un elemento. Ejemplo: Presidente o Presidenta del gobierno.
6. Clase vacía es la que no tiene ningún elemento. Se
representa: 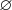
Operaciones con clases
Si tenemos varias clases, se puede establecer entre ellas varias operaciones semejantes a la lógica proposicional.
Suma Lógica
![A\cup B\, [ x \in A \lor x \in B ] A\cup B\, [ x \in A \lor x \in B ]](/images/math/math-e124513b48050a93d5a52f6de1d8b1aa.png)
Ejemplo: Los gatos y los seres grises = Todos los gatos y todos los seres grises, elefantes, trajes etc.
Producto lógico
Son los elementos comunes entre ambas clases:
![A\,\cap B\, [ x \in A \land x \in B ] A\,\cap B\, [ x \in A \land x \in B ]](/images/math/math-260d2219e8bd5ce56d43fdfa2ebbbf7d.png)
En el ejemplo anterior el producto lógico, son los gatos grises.
Diferencia lógica de clases
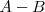 . Los elementos que pertenecen a A y no pertenecen a B.
. Los elementos que pertenecen a A y no pertenecen a B.
Los gatos que no son grises: ![A - B\, [ x \in A \land x \notin B ] A - B\, [ x \in A \land x \notin B ]](/images/math/math-3fcc53527037791f14815cec0795311b.png)
Diferencia simétrica de clases
Los elementos que pertenecen a 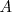 y que pertenecen a
y que pertenecen a 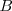 pero no a ambos:
pero no a ambos:
![A \Delta B \, [ x \in A \,\underline{\lor} \, x \in B ] A \Delta B \, [ x \in A \,\underline{\lor} \, x \in B ]](/images/math/math-0df39e32a7c989c9caf375a512fd15dd.png)
Clase complementaria
Si establecemos la clase 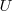 universal y otra
universal y otra 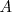 , que es subclase de
, que es subclase de 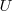 , la clase complementaria de
, la clase complementaria de 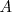 , es la clase constituida por los elementos que pertenecen a
, es la clase constituida por los elementos que pertenecen a 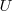 y no pertenecen a
y no pertenecen a 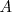 :
:
![\overline{A}\, [x\in U \land x\notin A] \overline{A}\, [x\in U \land x\notin A]](/images/math/math-b4c0a7bcc54ea83abfb76778349ff454.png)
Si tomamos como clase universal 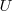 a los españoles y como clase
a los españoles y como clase 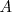 , los habitantes de la comunidad de Madrid, la clase complementaria son todos los españoles que no viven en la comunidad de Madrid.
, los habitantes de la comunidad de Madrid, la clase complementaria son todos los españoles que no viven en la comunidad de Madrid.
Leyes de la lógica de clases
Las más importantes son:
Idempotencia
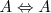
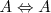
Conmutativa
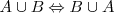
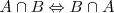
Asociativa
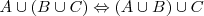
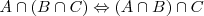
Distributiva
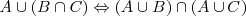
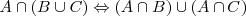
Identidad
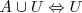
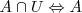
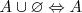
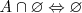
Complementaridad
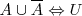
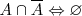
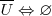
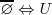
Doble Complementaridad
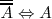
Leyes de Absorción
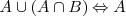

Leyes de Morgan


Las demostraciones de estas leyes se realizan por las tablas de pertenencia, semejantes a las tablas de verdad en la Lógica proposicional:
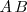 |
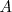 |
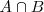 |
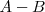 |
 |
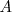 |
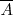 |
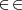 |
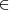 |
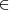 |
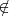 |
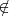 |
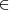 |
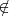 |
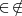 |
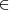 |
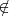 |
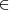 |
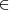 |
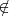 |
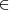 |
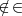 |
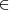 |
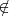 |
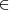 |
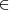 |
||
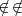 |
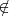 |
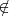 |
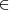 |
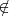 |
Puede verse el isomorfismo entre la suma lógica de clases y la disyunción de proposiciones, así como del producto lógico y la conjunción. La diferencia simétrica con la disyunción exclusiva y entre la clase complementaria y la negación
Tweet


