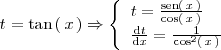Métodos de integración
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | |||
==Introducción== | ==Introducción== | ||
| Línea 186: | Línea 187: | ||
</center> | </center> | ||
se tiene que | se tiene que | ||
| + | <center> | ||
| + | <math> | ||
| + | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g} \left( | ||
| + | t \right) \cdot \mathrm{d}t | ||
| + | </math> | ||
| + | </center> | ||
| + | Supongamos que | ||
| + | <math> | ||
| + | \mathrm{G} \left( x \right) | ||
| + | </math> | ||
| + | es una primitiva de | ||
| + | | ||
| + | <math> | ||
| + | \mathrm{g} \left( x \right) | ||
| + | </math>, | ||
| + | entonces | ||
<center> | <center> | ||
<math> | <math> | ||
\int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
\mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( | ||
| - | t \right) \cdot \mathrm{d}t = \mathrm{g} \left( | + | t \right) \cdot \mathrm{d}t = \mathrm{g} \left( t \right) + C= \mathrm{g} \left( |
\, \mathrm{f} \left( x \right)\right) + C | \, \mathrm{f} \left( x \right)\right) + C | ||
</math> | </math> | ||
| Línea 221: | Línea 239: | ||
<math> | <math> | ||
\begin{array}{rl} | \begin{array}{rl} | ||
| - | \mathrm{g} \left( x \right) & = \cos \left( x \right) | + | \mathrm{g}^\prime \left( x \right) & = \mathrm{cos} \left( x \right) |
\\ | \\ | ||
t = \mathrm{f} \left( x \right) & = e^x | t = \mathrm{f} \left( x \right) & = e^x | ||
| Línea 235: | Línea 253: | ||
\\ | \\ | ||
\int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x & = & \int | \int e^x \cdot \cos \left( \, e^x \, \right) \cdot \mathrm{d}x & = & \int | ||
| - | \mathrm{g} \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x | + | \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Línea 241: | Línea 259: | ||
En este caso, una primitiva de | En este caso, una primitiva de | ||
<math> | <math> | ||
| - | \mathrm{g} \left( x \right) | + | \mathrm{g}^\prime \left( x \right) |
</math> | </math> | ||
es | es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \mathrm{ | + | \mathrm{g} \left( \, x \, \right) = \mathrm{sen} \left( \, x \, \right) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 253: | Línea 271: | ||
<math> | <math> | ||
\int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | \int \mathrm{g}^\prime \left( \, \mathrm{f} \left( x \right) \right) \cdot | ||
| - | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g} \left( | + | \mathrm{f}^\prime \left( x \right) \cdot \mathrm{d}x = \int \mathrm{g}^\prime \left( |
| - | t \right) \cdot \mathrm{d}t = \mathrm{ | + | t \right) \cdot \mathrm{d}t = \mathrm{g} \left( t \right) + C= \mathrm{G} \left( |
\mathrm{f} \left( x \right)\right) + C = \mathrm{sen} \left( e^x \right) + C | \mathrm{f} \left( x \right)\right) + C = \mathrm{sen} \left( e^x \right) + C | ||
</math> | </math> | ||
Revisión de 09:50 3 ene 2011
Tabla de contenidos |
Introducción
No todos los métodos de integración son adecuados para todas las integrales. La habilidad de ver cual es el método de integración mas idoneo para calcular una integral se adquiere resolviendo muchas integrales.
Integración por partes
La fórmula para la derivada de un producto es:
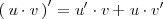
Despejando el último sumando, queda:
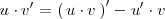
Si integramos en los dos miembros, se obtiene:
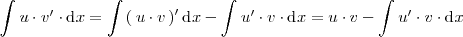
La última igualdad es cierta porque una primitiva de la derivada de una función es esa misma función.
Esta fórmula permite calcular la integral
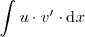 a partir de la integral
a partir de la integral
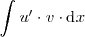 .
.
Para que sea de utilidad el utilizar este metodo es necesario que nos resulte
mas sencilla de resolver la integral
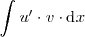 que la integral de partida,
que la integral de partida,
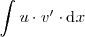 .
.
Ejemplo
Calculemos la integral
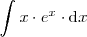
por partes.
Si hacemos
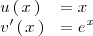
se tiene que
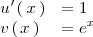
Utilizando la fórmula que hemos visto antes
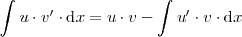
se deduce que
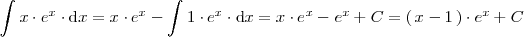
Método de sustitución
Supongamos que queremos resolver una integral del tipo:
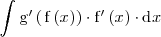
Una manera de resolver un problema de este tipo es haciendo el cambio de variable
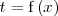
La nueva variable
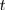 es una función de
es una función de
 ,
con lo cual podemos hablar de la derivada de
,
con lo cual podemos hablar de la derivada de
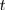 con respecto de
con respecto de
 , que se puede escribir como un cociente de diferenciales:
, que se puede escribir como un cociente de diferenciales:
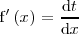
Despejando
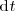 en la igualdad anterior, se deduce que
en la igualdad anterior, se deduce que
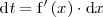
Sustituyendo
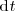 por
por
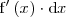 y
y
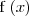 por
por
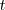 en
en
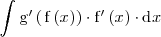
se tiene que
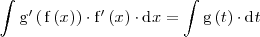
Supongamos que
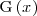 es una primitiva de
es una primitiva de
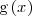 ,
entonces
,
entonces
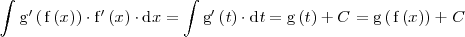
Las igualdades anteriores resumen en que consiste el metodo de sustitución. El
método de sustitución es util en tanto en cuanto sea relativamente facil encontrar una primitiva
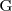 de
de
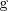 .
.
Ejemplo
Calculemos mediante el método de sustitución la integral
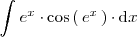
Para ello utilizamos las formulas dadas en la descripción del metodo de sustitución con
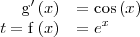
Observese que
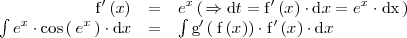
En este caso, una primitiva de
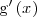 es
es
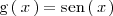
Por lo tanto
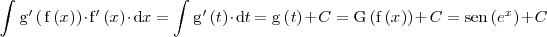
Integración de cocientes de polinomios
Sean
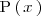 y
y
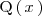 dos polinomios, entonces:
dos polinomios, entonces:
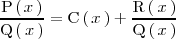
donde
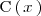 es un polinomio ( el cociente ) y
es un polinomio ( el cociente ) y
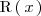 es otro polinomio ( el resto ) de grado menor al grado de
es otro polinomio ( el resto ) de grado menor al grado de
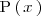 .
.
Si el grado de
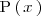 es menor que el grado de
es menor que el grado de
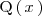 ,
entonces
,
entonces
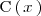 es cero y
es cero y
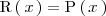 .
.
Como
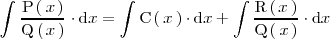
nos podemos restringir al caso en el que el grado del polinomio divisor,
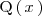 ,
es mayor que grado del polinomio dividendo,
,
es mayor que grado del polinomio dividendo,
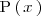 .
.
Para resolver este tipo de integrales lo primero que hay que hacer es
factorizar
el polinomio divisor
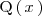 .
.
Al factorizar
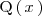 lo podemos poner como un producto de polinomios de grado
uno y/o de grado dos:
lo podemos poner como un producto de polinomios de grado
uno y/o de grado dos:
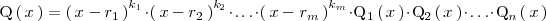
donde

son todas las raices reales de
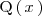 y
y
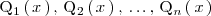
son polinomios de grado dos irreducibles ( sin raices reales ).
De esta forma
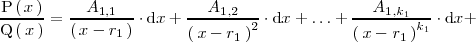
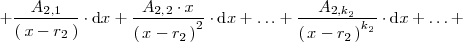
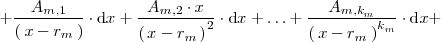
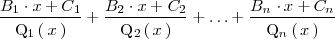
Donde hemos seguido la siguiente notación:
1
.
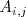 es la constante a la que divide
es la constante a la que divide
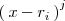 .
.
2
.
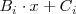 es el polinomio de grado uno al que divide
es el polinomio de grado uno al que divide
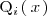 .
.
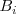 y
y
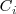 son constantes ( números reales que no dependen de
son constantes ( números reales que no dependen de
 ).
).
Por lo tanto, la integral de
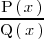 es la suma de las integrales de las fracciones mas simples en las que
hemos descompuesto
es la suma de las integrales de las fracciones mas simples en las que
hemos descompuesto
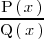 .
.
Estas integrales mas simples son casi inmediatas. Así
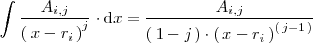
Esta integral se puede resolver utilizando el cambio de variable
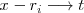 y la integral inmediata
y la integral inmediata
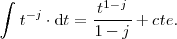
Por otra parte, la integral
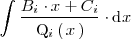
se resuelve descomponiendola en otras dos:
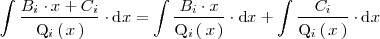
La primera de ellas se resuelve mediante el cambio de variable
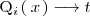 :
:
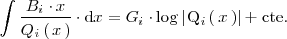
donde
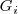 es una constante.
es una constante.
Para resolver la segunda integral ponemos el polinomio
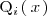 de la forma:
de la forma:

y hacemos el cambio de variable
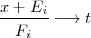 :
:
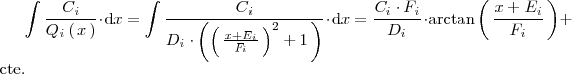
Ejemplo
Utilicemos el metodo que se acaba de describir para resolver la siguiente integral:
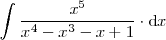
Como el polinomio dividendo ( el polinomio en el numerador,
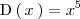 ) es de grado mayor que el polinomio divisor ( el polinomio en el
denominador,
) es de grado mayor que el polinomio divisor ( el polinomio en el
denominador,
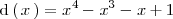 ), lo primero que hacemos es dividir ambos polinomios para obtener el
cociente
), lo primero que hacemos es dividir ambos polinomios para obtener el
cociente
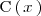 y el resto
y el resto
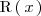 de la división.
de la división.
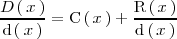
Al hacer la división obtenemos que
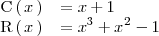
Por lo tanto
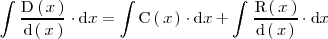
con
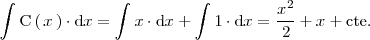
Pasemos ahora a resolver la integral
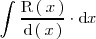 .
.
Para ello, lo primero que hacemos es factorizar el polinomio
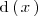 :
:
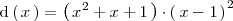
Con lo cual existen números reales
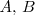 y
y
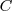 tales que:
tales que:
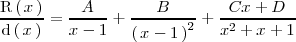
A continuación calculamos los valores de
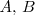 y
y
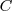 para que la igualdad anterior sea cierta:
para que la igualdad anterior sea cierta:
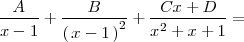
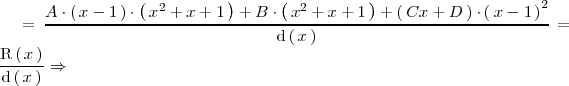
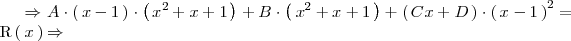
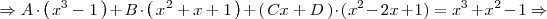
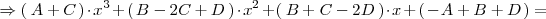
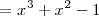
Dos polinomios son iguales si, y solo si, sus coeficientes y terminos independientes
son iguales ( ambos polinomios tienen el mismo grado, digamos
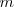 ,
y el coeficiente de
,
y el coeficiente de
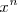 en uno de los polinomios es el coeficiente de
en uno de los polinomios es el coeficiente de
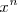 en el otro polinomio, para
en el otro polinomio, para
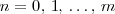 ). Así, se tiene que:
). Así, se tiene que:
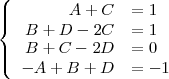
La solución de este sistema de ecuaciones es:
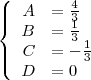
De este modo:
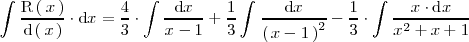
Las primeras dos integrales en el miembro de la derecha las podemos resolver con
el cambio de variable
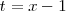 :
:
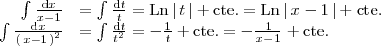
Para finalizar el ejemplo calculamos la última integral:
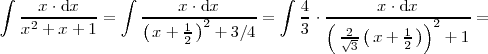
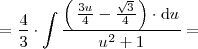
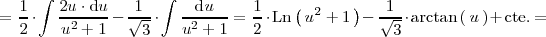
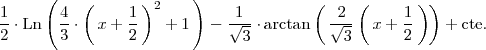
donde se ha utilizado el cambio de variable:
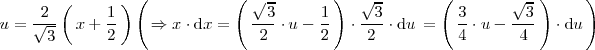
Integrales de funciones trigonométricas
Para resolver este tipo de integrales se utilizan amenudo las igualdades que se estudian
en trigonometría. Tambien se utilizan los cambios de variables
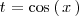 ,
,
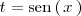 o
o
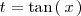 .
.
Ejemplo 1
Resolvamos la integral
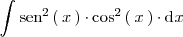
Para ello tenemos en cuenta que
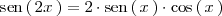
con lo cual
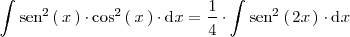
Como
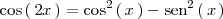
y como
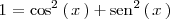
Despejando
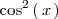 de esta última igualdad y sustituyendolo en la anterior, se tiene que
de esta última igualdad y sustituyendolo en la anterior, se tiene que
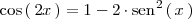
Sustituyendo en esta igualdad
 por
por
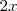 y despejando
y despejando
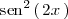 se llega a que
se llega a que
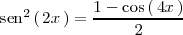
Así
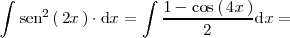
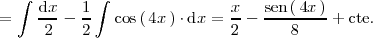
La última integral se calcula con el cambio de variable
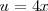 .
.
Ejemplo 2
Resolvamos ahora la siguiente integral:
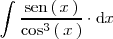
mediante el cambio de variable
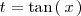
Definiendo
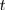 de esta manera resulta que
de esta manera resulta que
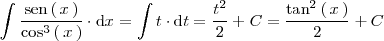
ya que