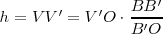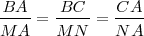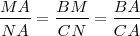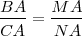|
m |
| (27 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | {{en desarrollo}}
| |
| - |
| |
| | ===Características generales=== | | ===Características generales=== |
| | | | |
| - | Consideramos que una variable <math>x</math> puede adquirir los valores <math>a,b,c,d,...</math> y otra variable y los valores <math>a' , b' , c' , d' , ...</math> <math>x</math> e <math>y</math> son directamente proporcionales si <math>a/a' = b/b' = c/c' = d/d'...</math> | + | Consideramos que una variable '''x''' puede adquirir los valores '''a,b,c,d,...''' y otra variable los valores '''a' , b' , c' , d' , ...''' '''x''' e '''y''' son directamente proporcionales si |
| | + | |
| | + | <math>\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'}...</math> |
| | | | |
| | ===Teorema de Tales=== | | ===Teorema de Tales=== |
| | | | |
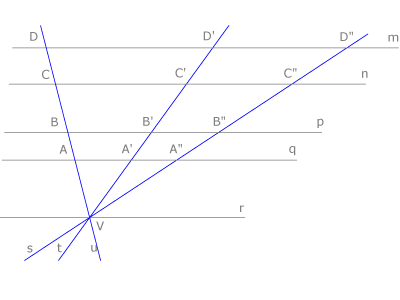
| - | Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: <math>VA/VA'=AB/A'B'=BC/B'C'=..........</math> | + | Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: |
| - | <math>VA'/VA''=A'B'/A''B''=B'C'/B''C''=.......</math> | + | |
| | + | <math>\frac{VA}{VA'} = \frac{AB}{A'B'} = \frac{BC}{B'C'} =..........</math> |
| | + | |
| | + | |
| | + | <math>\frac{VA'}{VA''} = \frac{A'B'}{A''B''} = \frac{B'C'}{B''C''} =.......</math> |
| | | | |
| | [[Imagen:21Proporcionalidaddirecta.gif]] | | [[Imagen:21Proporcionalidaddirecta.gif]] |
| Línea 14: |
Línea 18: |
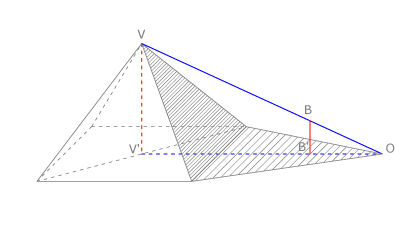
| | En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón <math>BB'</math>. | | En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón <math>BB'</math>. |
| | | | |
| - | En nuestra figura vemos que la altura <math>h = VV' </math> es la incógnita de esta igualdad: <math>VV ' / BB' = V 'O / B ' O </math>, luego | + | En nuestra figura vemos que la altura <math>h = VV' </math> es la incógnita de esta igualdad: |
| | | | |
| - | <math>h= VV' = V 'O \cdot BB' / B'O </math> | + | <math>\frac{VV'}{BB'} = \frac{V'O}{B'O}</math>, luego |
| | + | |
| | + | <math>h = VV' = V 'O \cdot \frac{BB'}{B'O}</math> |
| | | | |
| | [[Imagen:DibujoTecnico I-5 1.gif]] | | [[Imagen:DibujoTecnico I-5 1.gif]] |
| Línea 22: |
Línea 28: |
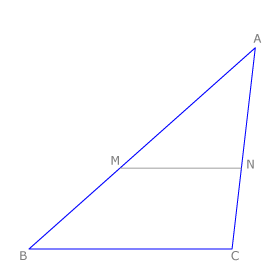
| | El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que: | | El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que: |
| | | | |
| - | <math>BA/MA = BC/MN = CA/NA</math> | + | <math>\frac{BA}{MA} = \frac{BC}{MN} = \frac{CA}{NA}</math> |
| | | | |
| - | <math>MA/NA=BM/CN= BA/CA</math> | + | <math>\frac{MA}{NA} = \frac{BM}{CN} = \frac{BA}{CA}</math> |
| | | | |
| | De la primera igualdad deducimos la segunda ya que: | | De la primera igualdad deducimos la segunda ya que: |
| | | | |
| - | <math>BA/CA = MA/NA</math> | + | <math>\frac{BA}{CA} = \frac{MA}{NA}</math> |
| | | | |
| | [[Imagen:DibujoTecnico I-5 2.gif]] | | [[Imagen:DibujoTecnico I-5 2.gif]] |
| - |
| |
| - | ===Aplicaciones del teorema de Tales===
| |
| - |
| |
| - | Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la tercera proporcional de dos segmentos dados, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones.
| |
| - |
| |
| - | ====División de un segmento en partes proporcionales====
| |
| - |
| |
| - | Para dividir un segmento '''AD ''' en partes proporcionales a las partes '''A’B’, B’C’ y C’D’ ''' dadas, trazamos una recta que pase por '''A''' definiendo así un haz de dos rectas. Sobre ella llevamos las magnitudes dadas. Por el extremo '''D’ ''' trazamos la recta '''DD’ '''. Trazamos paralelas a '''DD’ ''' por los puntos '''B’''' y '''C’ '''. Estas paralelas cortan al segmento dado en los puntos '''B''' y '''C'''.
| |
| - | Por el teorema de Tales, se cumplirá que '''AB/A’B’=BC/B’C’=CD/C’D’'''.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 3.gif]]
| |
| - |
| |
| - | ====División de un segmento en partes iguales. ====
| |
| - |
| |
| - | Para dividir un segmento '''AB''' dado en '''n''' partes iguales, trazamos una recta que pase por '''A'''.
| |
| - | Situamos sobre ella '''n''' partes iguales, que numeramos. En este caso '''n=9'''. Dibujamos la recta '''9B''' y trazamos paralelas a ella por los puntos restantes, ordenadamente.
| |
| - |
| |
| - | Por ser equidistantes las paralelas los segmentos definidos sobre '''AB''' son iguales.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 4.gif]]
| |
| - |
| |
| - | ====Demostración del teorema de la bisectriz====
| |
| - |
| |
| - | La bisectriz del ángulo '''BAC''' de un triángulo '''ABC''' divide a su lado opuesto en partes proporcionales a los otros lados del triángulo.
| |
| - | Consideramos el triángulo '''ABC''' y su bisectriz '''AD'''. Según el teorema: '''BD/DC=AB/AC. '''
| |
| - |
| |
| - | Vamos a comprobarlo:
| |
| - |
| |
| - | Trazamos por '''C''' una paralela a '''AD''', que corta a la prolongación de '''AB''' en '''E'''.
| |
| - |
| |
| - | Por el teorema de Tales, se cumple que: '''BD/DC=AB/AE'''.
| |
| - |
| |
| - | Los ángulos '''BAD=AEC''' por tener un lado común y los otros paralelos entre sí y '''DAC=ACE''' por ser alternos internos.
| |
| - |
| |
| - | Como '''BAD=DAC''' tenemos que '''AEC=ACE''', lo que indica que el triángulo '''ACE''' es isósceles con base '''EC''', luego '''AC=AE'''.
| |
| - |
| |
| - | Lo aplicamos a la igualdad anterior y resulta que '''BD/DC=AB/AC'''.
| |
| - |
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 5.gif]]
| |
| - |
| |
| - | El mismo razonamiento vale si consideramos la bisectriz del ángulo exterior '''MAC. '''
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 6.gif]]
| |
| - |
| |
| - | ====Cuarta proporcional de tres segmentos====
| |
| - |
| |
| - | Dados tres segmentos '''a, b y c''', se llama magnitud '''cuarta proporcional''' de ellos a un segmento '''d''' que verifica: '''a/b=c/d'''.
| |
| - |
| |
| - | Para hallarlo aplicamos el teorema de Tales: dibujamos un haz de dos rectas. Sobre una de las rectas situamos los segmentos '''a''' y '''c''' y sobre la otra el segmento '''b''', como se ve en la figura.
| |
| - |
| |
| - | Trazamos la recta que une los extremos de '''a''' y '''b''' y trazamos una paralela por el extremo de '''c'''. Esta paralela define el segmento d solución del problema, pues: '''a/b=c/d'''
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 7.gif]]
| |
| - |
| |
| - | ====Tercera proporcional de dos segmentos====
| |
| - |
| |
| - | Dados dos segmentos '''a''' y '''b''', se llama magnitud '''tercera proporcional''' de ellos a un segmento c que verifica: '''a/b=b/c'''.
| |
| - |
| |
| - | Vemos que es un caso particular de cuarta proporcional, con los términos intermedios iguales.
| |
| - |
| |
| - | Para hallarlo aplicamos el teorema de Tales: dibujamos un haz de dos rectas. Sobre una de las rectas situamos los segmentos '''a''' y '''b''' y sobre la otra el segmento '''b''', como se ve en la figura.
| |
| - |
| |
| - | Trazamos la recta que une los extremos de '''a''' y '''b''' y trazamos una paralela por el extremo de '''b'''. Esta paralela define el segmento c solución del problema, pues: '''a/b=b/c'''
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 8.gif]]
| |
| - |
| |
| - | ====La proporción áurea====
| |
| - |
| |
| - | Cuando en una tercera proporcional el término mayor es igual a la suma de los otros dos se verifica que:
| |
| - |
| |
| - | <math>a + \frac{b}{a} = \frac{a}{b} = \Phi = \frac{(1 + \sqrt 5)}{2}</math>
| |
| - |
| |
| - |
| |
| - | <math>\Phi = 1,...........= \frac{(1 + \sqrt 5)}{2}</math> es el número de oro.
| |
| - |
| |
| - | Cuando un rectángulo tiene los lados con esta proporción recibe el nombre de '''rectángulo de oro'''. En el capítulo dedicado a las relaciones del arte con la geometría veremos la importancia de <math>\Phi</math> en el estudio de las proporciones armónicas. Más adelante estudiaremos las espirales relacionadas con el rectángulo de oro.
| |
| - |
| |
| - | También es fundamental para la construcción del pentágono regular, pues la proporción áurea se cumple entre su diagonal y su lado:
| |
| - |
| |
| - | <math>\frac{d}{l} = \Phi</math>
| |
| - |
| |
| - | Vamos a comprobar que
| |
| - |
| |
| - | <math>a + \frac{b}{a} = \frac{a}{b} = \Phi = \frac{(1+ \sqrt{5})}{2}</math>
| |
| - |
| |
| - | Operamos:
| |
| - |
| |
| - | <math>(a+b) \cdot b = a^2</math>
| |
| - |
| |
| - | <math>ab + b2 = a^2</math>
| |
| - |
| |
| - | <math>a^2 – ab – b^2 = 0</math>
| |
| - |
| |
| - | Resulta una ecuación de segundo grado donde la incógnita es a. Vamos a despejarla. Nos interesa sólo la raíz positiva:
| |
| - |
| |
| - | <math>a = \frac{b + \sqrt{(b^2 + 4b^2)} }{2} = b \frac{ (1 + \sqrt{5})}{2}</math>
| |
| - |
| |
| - | <math> \frac{a}{b} = \Phi = \frac{1+ \sqrt{5}}{2}</math>
| |
| - |
| |
| - | Vamos a construir segmentaciones áureas a partir de diferentes datos:
| |
| - |
| |
| - | =====Cuando el dato es a=====
| |
| - |
| |
| - | Dibujamos un cuadrado de lado '''a''' y la mediatriz de dicho lado. Con centro en '''N''', punto medio de '''a''', y radio '''NM''', diagonal de medio cuadrado, trazamos un arco que corta en '''P''' a la prolongación de '''a''', definiendo el segmento '''b'''. Se cumple que <math>\frac{a}{b} = \Phi</math>
| |
| - |
| |
| - | Vamos a comprobarlo:
| |
| - |
| |
| - | Como <math>MN = NP</math>, pues son radios de la misma circunferencia, resulta que:
| |
| - |
| |
| - | Consideramos el triángulo '''MNQ''', por Pitágoras:
| |
| - |
| |
| - | <math>MN = \sqrt{a^2 + \frac{a^2}{4}} = \sqrt{\frac{5a^2}{4}} = {\frac{a\sqrt{5}}{2}</math>
| |
| - |
| |
| - | En nuestro dibujo:
| |
| - |
| |
| - | <math>NP = \frac{a}{2} +b</math>
| |
| - |
| |
| - | Lo aplicamos en la igualdad anterior:
| |
| - |
| |
| - | <math>\frac{a}{2} + b = \frac{a \sqrt {5}}{2}</math>
| |
| - |
| |
| - | <math>b = \frac{a \sqrt{5}}{2} - \frac{a}{2} = a \frac{\sqrt {5} -1}{2}</math>
| |
| - |
| |
| - | luego:
| |
| - |
| |
| - | <math>a = \frac{2b}{\sqrt {5} -1}</math>
| |
| - |
| |
| - | <math>\frac{a}{b} = \frac{2}{\sqrt {5} -1} = \frac{2 (\sqrt {5} +1)}{(\sqrt {5} +1) (\sqrt {5} - 1)} = \frac{2 (1+\sqrt{5})}{4} = \frac{(1+\sqrt{5})}{2} = \Phi</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 9.gif]]
| |
| - |
| |
| - | =====Cuando el dato es a+b=====
| |
| - |
| |
| - | Ésta es otra construcción de la segmentación áurea. Sea '''MN= a+b'''. Trazamos un segmento perpendicular de magnitud '''MN/2''' y dibujamos el triángulo rectángulo '''MNP'''. Con centro en '''P''' y radio '''PN''' trazamos un arco que corta a la hipotenusa en el punto '''Q'''. Con centro en A trazamos un arco de radio '''AQ''' que corta a '''MN''' en el punto '''R''', definiendo los segmentos '''a''' y '''b'''.
| |
| - |
| |
| - | Se verifica que: <math>\frac{a}{b} = \Phi</math>
| |
| - |
| |
| - | Vamos a comprobarlo:
| |
| - |
| |
| - | <math>MP = a + \frac{a+b}{2}</math>, ya que
| |
| - |
| |
| - | <math>MQ =a</math> y <math>PQ = \frac{a+b}{2}</math>
| |
| - |
| |
| - | Considerando el triángulo '''MNP''', por Pitágoras:
| |
| - |
| |
| - | <math>MP^2 = (a+b)^2 + \left (\frac{a+b}{2} \right )^2 = \frac{5 (a+b)^2} {4}</math>, luego:
| |
| - |
| |
| - | <math>MP = \frac{(a+b)\sqrt{5}}{2}</math>
| |
| - |
| |
| - | <math>MP = a + \frac{a+b}{2} = \frac{(a+b)\sqrt{5}}{2}</math>
| |
| - |
| |
| - | <math>a = (a+b) \frac{\sqrt{5} -1}{2}</math>
| |
| - |
| |
| - | <math>\frac{(a+b)}{a} = \frac{2}{\sqrt{5}-1} = \frac{2 (\sqrt{5}+1) }{ (\sqrt{5}+1) (\sqrt{5}-1)} = \frac{2(1+\sqrt{5})}{4} = \frac{(1+\sqrt{5})}{2}= \Phi</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 10.gif]]
| |
| - |
| |
| - |
| |
| - | =====Los rectángulos de oro=====
| |
| - |
| |
| - | Si el dato es el lado menor '''a''' usamos la primera construcción de segmentación áurea.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 11.gif]]
| |
| - |
| |
| - | Si el dato es el lado mayor, '''a+b''', utilizamos la segunda.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 12.gif]]
| |
| - |
| |
| - | ====El teorema de Euclides====
| |
| - |
| |
| - | Ya vimos el '''teorema de Euclides''', considerando su enunciados como teoremas de la '''altura''' y del '''cateto''', en el capítulo de triángulos y realizamos sus demostraciones gráficas.
| |
| - |
| |
| - | Ahora vamos a ver su relación con la '''tercera proporcional'''. Si consideramos que:
| |
| - |
| |
| - | <math>\frac{a}{x}=\frac{x}{b}</math>
| |
| - |
| |
| - | vemos que el término intermedio, '''x''', es media proporcional entre '''a''' y '''b''', pues:
| |
| - |
| |
| - | <math>x^2 = ab</math>
| |
| - |
| |
| - | Las construcciones de la media proporcional de dos segmentos, basadas directamente en '''Euclides''', tienen muchas aplicaciones en la resolución de problemas gráficos.
| |
| - |
| |
| - | =====Aplicando el teorema de la altura=====
| |
| - |
| |
| - | Dibujamos el segmento '''BC= a+b''', como vemos en la figura. Trazamos la semicircunferencia de diámetro '''BC'''. Por el extremo común de los segmentos, '''H''', dibujamos la perpendicular a '''BC''' que corta al arco en '''A'''.
| |
| - | '''AH''' es la '''altura''' de '''ABC''' y es media proporcional de los segmentos en que divide a la hipotenusa: '''a y b''', como ya vimos en el capítulo 2.
| |
| - |
| |
| - | <math>AH = \sqrt{ab}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 13.gif]]
| |
| - |
| |
| - | =====Aplicando el teorema del cateto=====
| |
| - |
| |
| - | Dibujamos el segmento '''BC=b''' y '''BH=a''', superpuestos, como vemos en la figura. Trazamos la semicircunferencia de diámetro '''BC'''. La perpendicular a '''BC''' desde '''H''' corta al arco en '''A'''.
| |
| - |
| |
| - | El '''cateto AB''' es media proporcional su proyección sobre la hipotenusa, '''a''' , y de la hipotenusa, '''b''', como ya vimos en el capítulo 2.
| |
| - |
| |
| - | <math>AB = \sqrt{ab}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 14.gif]]
| |
| - |
| |
| - |
| |
| - | ====Aplicaciones al cálculo gráfico====
| |
| - |
| |
| - | Para resolver estos problemas debemos definir la unidad que consideramos.
| |
| - |
| |
| - |
| |
| - | =====División de dos segmentos: c=a/b=====
| |
| - |
| |
| - | Dados los segmentos '''a''' y '''b''' hallamos un tercer segmento c que cumpla: '''c=a/b''', siendo la unidad el centímetro.
| |
| - |
| |
| - | Dibujamos un haz de dos rectas que se cortan en '''O'''. Sobre una de ellas llevamos '''ON=a''' y sobre la otra '''OM=b y MP=1cm''' (segmento unidad), como vemos en la figura. Dibujamos '''MN''' y su paralela por '''P, PQ'''.
| |
| - |
| |
| - | <math>NQ=c</math>
| |
| - |
| |
| - | Vemos que se cumple:
| |
| - |
| |
| - | <math>c=\frac{a}{b}</math> pues:
| |
| - |
| |
| - | <math>\frac{a}{b}=\frac{c}{1}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 15.gif]]
| |
| - |
| |
| - | =====Producto de dos segmentos: c=ab=====
| |
| - |
| |
| - | Dados los segmentos '''a''' y '''b''' hallamos un tercer segmento c que cumpla: '''c=ab''', siendo la unidad el centímetro.
| |
| - |
| |
| - | Dibujamos un haz de dos rectas que se cortan en '''O'''. Sobre una de ellas llevamos '''ON=a''' y sobre la otra '''OM=1cm''' (segmento unidad) y '''MP=b''', como vemos en la figura. Dibujamos '''MN''' y su paralela por '''P, PQ'''.
| |
| - |
| |
| - | <math>NQ=c</math>
| |
| - |
| |
| - | Vemos que se cumple:
| |
| - |
| |
| - | <math>c=ab</math>
| |
| - |
| |
| - | pues:
| |
| - |
| |
| - | <math>\frac{a}{1}=\frac{c}{b}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 16.gif]]
| |
| - |
| |
| - | =====Cuadrado de un segmento: b=a²=====
| |
| - |
| |
| - | Dado un segmento '''a''' hallamos un segmento '''b''' que cumpla <math>b=a^2</math>, siendo la unidad el centímetro.
| |
| - |
| |
| - | Esta construcción una variante de la del producto de un segmento.
| |
| - |
| |
| - | Dibujamos un haz de dos rectas que se cortan en '''O'''. Sobre una de ellas llevamos '''ON=a''' y sobre la otra '''OM=1cm''' (segmento unidad) y '''MP=a''', como vemos en la figura. Dibujamos '''MN''' y su paralela por '''P, PQ'''.
| |
| - |
| |
| - | <math>NQ=b</math>
| |
| - |
| |
| - | Vemos que se cumple:
| |
| - |
| |
| - | <math>b=a^2</math> ,pues:
| |
| - |
| |
| - |
| |
| - | <math>\frac{a}{1} = \frac{b}{a}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 17.gif]]
| |
| - |
| |
| - | =====Raíz cuadrada de un segmento: b=√a=====
| |
| - |
| |
| - | Dado un segmento '''a''' hallamos un segmento '''b''' que cumpla <math>b= \sqrt{a}</math>, siendo la unidad el centímetro
| |
| - |
| |
| - | Aplicamos el teorema de la '''altura''':
| |
| - |
| |
| - | Dibujamos el segmento '''BC''', siendo '''BH = 1cm''' (segmento unidad) y '''HC=a'''.
| |
| - |
| |
| - | Trazamos la semicircunferencia de diámetro '''BC'''. La perpendicular a '''BC''' por '''H''' corta al arco en '''A'''.
| |
| - |
| |
| - | <math>AH =b = \sqrt{a}</math>
| |
| - |
| |
| - | pues '''b''' es media proporcional de '''a''' y de '''la unidad'''.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 18.gif]]
| |
| - |
| |
| - | Esta construcción también se hace aplicando el teorema del '''cateto''', como puede verse en la figura.
| |
| - |
| |
| - | En este caso se dibuja el segmento '''BH=1cm''' y el segmento '''BC=a'''.
| |
| - |
| |
| - | Dibujamos la circunferencia de diámetro '''BC'''. Trazamos la perpendicular a '''BC''' desde '''H'''. Esta recta corta a la circunferencia en '''A'''.
| |
| - |
| |
| - | La magnitud solución es <math>AB = \sqrt{a}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 19.gif]]
| |
| - |
| |
| - | ====Cuadrado de un segmento, aplicando Euclides====
| |
| - |
| |
| - | Aplicamos el teorema de la altura:
| |
| - |
| |
| - | Dibujamos el segmento '''BH = 1cm''' (segmento unidad) y prolongamos la recta que lo contiene.
| |
| - |
| |
| - | Trazamos la perpendicular a '''BH''' por '''H''' y llevamos la magnitud '''a''' sobre ella:
| |
| - |
| |
| - | <math>AH = a</math>
| |
| - |
| |
| - | Dibujamos el arco de circunferencia que pasa por '''A''' y '''B''' y tiene el centro en la recta definida por '''BH'''. Su centro estará en la intersección de la mediatriz de '''AB''' con dicha recta. El arco corta a la recta en '''C'''.
| |
| - |
| |
| - | <math>HC= b = a^2</math>, pues <math>AH=a</math> es media proporcional de <math>b=a^2</math> y de la '''unidad'''.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 20.gif]]
| |
| - |
| |
| - | Esta construcción también se hace aplicando el teorema del '''cateto''', como puede verse en la figura.
| |
| - | En este caso se dibuja el segmento '''BH=1cm''' y se prolonga la recta que lo contiene. Se dibuja la perpendicular a dicha recta desde '''H''' y, con centro en '''B''' y radio '''a''' se traza el arco que la corta en '''A'''.
| |
| - |
| |
| - | Dibujamos la circunferencia que pasa por '''A''' y '''B''' y tiene el centro en la recta '''BH''': trazamos la mediatriz de '''AB''' que corta a dicha recta en su centro.
| |
| - |
| |
| - | '''BC''' es la magnitud solución: <math>BC=a^2</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 21.gif]]
| |
| - |
| |
| - | ====Razón simple y razón doble de puntos alineados====
| |
| - |
| |
| - | En primer lugar definimos el concepto de '''segmentos orientados'''. Son positivos los segmentos cuya nomenclatura indica un sentido, siguiendo el orden alfabético y son negativos cuando indica el sentido contrario.
| |
| - |
| |
| - | Por ejemplo: si '''AB''' es '''positivo''', '''BA''' será '''negativo'''.
| |
| - |
| |
| - | La '''razón simple''' y la '''razón doble''' operan con '''segmentos orientados'''.
| |
| - |
| |
| - | =====Razón simple=====
| |
| - |
| |
| - | Se llama '''razón simple''' de tres puntos alineados '''A, B y C''' y se nota '''(ABC)''' a la siguiente igualdad:
| |
| - | '''(ABC) = AB/AC''', siendo '''AB y AC''' segmentos orientados.
| |
| - |
| |
| - | Para construir una '''razón simple''' aplicamos lo aprendido en proporcionalidad directa:
| |
| - |
| |
| - | '''Ejemplo de razón positiva:''' Dado un segmento '''AB''', hallar el punto '''C''' que cumpla: '''(ABC) = 3'''.
| |
| - |
| |
| - | Dibujamos el segmento '''AB''' y trazamos por '''A''' una recta. Sobre ella situamos un punto '''X''', tal que '''AX = 3''' (unidades arbitrarias) y un punto '''Y''' tal que '''AY = 1''' (la unidad considerada).
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{AB}{AC} = \frac{AX}{AY} = \frac{3}{1}</math>, luego <math>(ABC) = 3</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 22.gif]]
| |
| - |
| |
| - | '''Ejemplo de razón negativa:''' Dado '''un segmento '''AB''', hallar el punto '''C''' que cumpla:
| |
| - |
| |
| - | <math>(ABC) = - \frac{p}{q}</math>, siendo '''p''' y '''q''' segmentos dados.
| |
| - |
| |
| - | Dibujamos el segmento '''AB''' y trazamos por '''A''' una recta. Sobre ella situamos un punto '''X''', tal que '''AX = p''' y un punto '''Y''' tal que '''AY =q''', teniendo en cuenta que '''AX''' y '''AY''' deben indicar sentidos contrarios para que la razón sea negativa.
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{AB}{AC} = - \frac{AX}{AY} = -\frac{p}{q}</math>, luego
| |
| - |
| |
| - | <math>(ABC) = - \frac{p}{q}</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 23.gif]]
| |
| - |
| |
| - |
| |
| - | =====Razón doble=====
| |
| - |
| |
| - | Se llama razón doble de cuatro puntos alineados '''A, B, C y D''' y se nota '''(ABCD)''' a la siguiente igualdad:
| |
| - |
| |
| - | <math>(ABCD) = \frac{(ACD)}{(BCD)} = \left (\frac{AC}{AD} \right ) : \left (\frac{BC}{BD} \right ) =</math>
| |
| - |
| |
| - | <math> \left (\frac{AC}{AD} \right ) \cdot \left (\frac{BD}{BC} \right ) = \left (\frac{AC}{BC} \right ) \cdot \left (\frac{BD}{AD} \right )</math>
| |
| - |
| |
| - | siendo <math>AC, AD, BC</math> y <math>BD</math> segmentos orientados.
| |
| - |
| |
| - | Para construir una razón doble aplicamos lo aprendido en proporcionalidad directa:
| |
| - |
| |
| - | '''Ejemplo de razón positiva:'''
| |
| - |
| |
| - | Dados los puntos alineados '''A, B y C''', hallar el punto '''D''' que cumpla:
| |
| - | '''(ABCD) =p/q''', siendo '''p''' y '''q''' segmentos dados.
| |
| - |
| |
| - | Para resolver gráficamente estos problemas debemos combinar haces de rectas con los vértices en '''C''' y en '''D''' como se ve a continuación.
| |
| - |
| |
| - | Trazamos por '''B''' una recta. Sobre ella situamos un punto '''X''', tal que '''BX = p''' y un punto '''Y''' tal que '''BY = q'''.
| |
| - |
| |
| - | Dibujamos la recta '''CY''' y trazamos una paralela a '''BY''' por '''A'''. Estas rectas se cortan en '''Z'''.
| |
| - |
| |
| - | '''AZ = n'''
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{q}{n} = \frac{BC}{AC}</math>
| |
| - |
| |
| - | Por otra parte, la recta '''ZX''' corta a la recta dato en '''D'''.
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{p}{n} = \frac{BD}{AD}</math>, luego:
| |
| - |
| |
| - | <math>(ABCD) = \frac{p}{q} = \left (\frac{BD}{AD} \right ) : \left ( \frac{BC}{AC} \right ) = \left ( \frac{AC}{BC} \right ) \cdot \left ( \frac{BD}{AD} \right )</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 24.gif]]
| |
| - |
| |
| - | '''Ejemplo de razón negativa:'''
| |
| - |
| |
| - | Dados los puntos alineados '''A, B y C''', hallar el punto '''D''' que cumpla:
| |
| - |
| |
| - | <math>(ABCD) = - \frac{p}{q}</math>, siendo <math>p</math> y <math>q</math> segmentos dados.
| |
| - |
| |
| - | Trazamos por '''A''' una recta. Sobre ella situamos un punto '''X''', tal que '''AX = p''' y un punto '''Y''' tal que '''AY = q''', teniendo en cuenta que los sentidos de '''AX''' y '''AY''' sean contrarios.
| |
| - |
| |
| - | Dibujamos la recta '''CX''' y trazamos una paralela a '''AX''' por '''B'''. Estas rectas se cortan en '''Z'''.
| |
| - | '''BZ = n'''.
| |
| - |
| |
| - | Se cumple que:
| |
| - | <math>\frac{p}{n} = \frac{AC}{BC}</math>
| |
| - |
| |
| - | Por otra parte, la recta '''ZY''' corta a la recta dato en '''D'''.
| |
| - |
| |
| - | Se cumple que:
| |
| - | <math>\frac{q}{n} = \frac{AD}{-BD}</math>, luego:
| |
| - |
| |
| - | <math>(ABCD) =-\frac{p}{q} = \left ( \frac{AC}{BC}\right ) : \left ( \frac{AD}{BD}\right ) = \left ( \frac{AC}{BC} \right ) \cdot \left ( \frac{BD}{AD} \right ) </math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 25.gif]]
| |
| - |
| |
| - | =====Cuaterna armónica=====
| |
| - |
| |
| - | Se llama cuaterna armónica a la razón doble de cuatro puntos alineados '''A, B, C y D''' que vale '''-1''':
| |
| - |
| |
| - | '''(ABCD) = -1'''
| |
| - |
| |
| - | '''Ejemplo de cuaterna armónica:'''
| |
| - |
| |
| - | Dados los puntos alineados '''A, B y C''', hallar el punto '''D''' que cumpla:
| |
| - |
| |
| - | '''ABCD) = -1'''
| |
| - |
| |
| - | Trazamos por '''A''' una recta. Sobre ella situamos dos puntos '''X''' e '''Y''', tal que '''AX = AY''', teniendo en cuenta que los sentidos de '''AX''' y '''AY''' sean contrarios.
| |
| - |
| |
| - | Dibujamos la recta '''CX''' y trazamos una paralela a '''AX''' por '''B'''. Estas rectas se cortan en '''Z'''.
| |
| - |
| |
| - | '''BZ = n'''
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{AX}{n} = \frac{AC}{BC}</math>
| |
| - |
| |
| - | Por otra parte, la recta '''ZY''' corta a la recta dato en '''D'''.
| |
| - |
| |
| - | Se cumple que:
| |
| - |
| |
| - | <math>\frac{AY}{n} = \frac{AX}{n} = \frac{AD}{-BD}</math>, luego:
| |
| - |
| |
| - | <math>\frac{-AX}{n} = \frac{AD}{BD}</math>
| |
| - |
| |
| - | <math>(ABCD) = \frac{AX}{-AX}= -1</math>
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 26.gif]]
| |
| - |
| |
| - | ====Escalas====
| |
| - |
| |
| - | Se llama escala a la razón entre una magnitud dibujada y su magnitud real.
| |
| - |
| |
| - | '''E = magnitud de un segmento dibujado/ magnitud real del segmento.'''
| |
| - |
| |
| - | Si nos dicen que el segmento '''AB''', que mide 3 cm, representa una distancia de 300 Km y nos preguntan a qué escala está representado, aplicamos la definición:
| |
| - | Escala = 3cm/ 300Km
| |
| - |
| |
| - | A continuación igualamos las unidades:
| |
| - |
| |
| - | <math>Escala = \frac{3cm}{300Km} = \frac{3cm}{30000000cm} = \frac{1}{10.000.000}</math>
| |
| - |
| |
| - | Cuando una escala representa a los objetos reduciendo su tamaño se llama '''escala de reducción''', cuando lo amplía, se llama '''escala de ampliación''', cuando representa un objeto a tamaño real se llama '''escala real'''.
| |
| - |
| |
| - | Se llaman '''escalas gráficas o escalas volantes''' a las reglas que nos permiten medir en las diferentes escalas.
| |
| - |
| |
| - | '''Construcción de una escala gráfica de ampliación:'''
| |
| - |
| |
| - | Si nos indican que el segmento '''AB''' representa '''3mm''', al dividirlo en 3 partes iguales tendremos el segmento que representa '''1mm'''.
| |
| - |
| |
| - | Con este segmento como unidad construimos nuestra escala.
| |
| - |
| |
| - | A continuación construimos la '''contraescala''' dividiendo una unidad en 10 partes iguales. Así podremos medir décimas de milímetro.
| |
| - |
| |
| - | [[Imagen:DibujoTecnico I-5 27.gif]]
| |
| | | | |
| | | | |
| | [[Categoría:Dibujo]] | | [[Categoría:Dibujo]] |
Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas:
En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón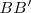 
.
El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que:
Navegación
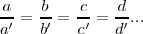
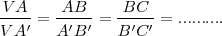
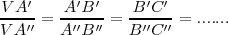
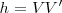es la incógnita de esta igualdad:
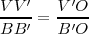, luego
