Discontinuidades
De Wikillerato
| Línea 42: | Línea 42: | ||
\frac{x^2 \, - \, 1}{x \, + \, 1} & , & \quad \makebox{si}\quad x \neq 1 | \frac{x^2 \, - \, 1}{x \, + \, 1} & , & \quad \makebox{si}\quad x \neq 1 | ||
\\ | \\ | ||
| - | + | 2 & , & \quad \makebox{si} \quad x \, = \, 1 | |
\end{array} | \end{array} | ||
\right. | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | no es continua en el punto | ||
| + | <math> | ||
| + | x \, = \, 1 | ||
| + | </math> | ||
| + | porque | ||
| + | <math> | ||
| + | \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) \, = \, 0 | ||
| + | </math> | ||
| + | mientras que | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, 1 \, \right) \, = \, 2 | ||
| + | </math> | ||
| + | , es decir: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) \, \neq \, | ||
| + | \mathrm{f} \left( \, 1 \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como | ||
| + | <math> | ||
| + | \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | existe, la discontinuidad que | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene en el punto | ||
| + | <math> | ||
| + | x \, = \, 1 | ||
| + | </math> | ||
| + | es evitable. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función presenta una '''''discontinuidad de primera especie''''' en el punto | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | si los limites laterales de | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | en | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | existen pero son distintos, es decir: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right) \, \neq \, | ||
| + | \lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | definida por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) \, = \, | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x | ||
| + | \\ | ||
| + | x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | no es continua en el punto | ||
| + | <math> | ||
| + | x \, = \, 1 | ||
| + | </math> | ||
| + | porque | ||
| + | <math> | ||
| + | \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | no existe, al ser ambos limites laterales distintos: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to 1^+} \mathrm{f} \left( \, x \, \right) \, = \, 0 | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \lim_{x \to 1^-} \mathrm{f} \left( \, x \, \right) \, = \, 2 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como ambos limites laterales existen la discontinuidad que | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene en el punto | ||
| + | <math> | ||
| + | x \, = \, 1 | ||
| + | </math> | ||
| + | es de primera especie. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | presenta una '''''discontinuidad de segunda especie''''' en el punto | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | si no existe alguno de los limites laterales de | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | en dicho punto. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | definida por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) \, = \, | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | \frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x | ||
| + | \\ | ||
| + | 1 & , & \quad \makebox{si} \quad x \, > \, 0 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | no es continua en el punto | ||
| + | <math> | ||
| + | x \, = \, 0 | ||
| + | </math> | ||
| + | porque | ||
| + | <math> | ||
| + | \lim_{x \to 0} \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | no existe, al no existir el limite por la izquierda de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | cuando | ||
| + | <math> | ||
| + | x \to 0 | ||
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to 0^-} \mathrm{f} \left( \, x \, \right) \, = \, -\infty | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como este limite por la izquierda no existe | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene en el punto | ||
| + | <math> | ||
| + | x \, = \, 1 | ||
| + | </math> | ||
| + | una discontinuidad de segunda especie. | ||
<br/> | <br/> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 14:35 11 ene 2007
Una función es discontinua en un punto
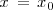 si
si
 no es continua en dicho punto.
no es continua en dicho punto.
Una función
 tiene una discontinuidad evitable en un punto
tiene una discontinuidad evitable en un punto
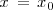 cuando existe el limite de la función en dicho punto.
cuando existe el limite de la función en dicho punto.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, + \, 1} & , & \quad \makebox{si}\quad x \neq 1
\\
2 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, + \, 1} & , & \quad \makebox{si}\quad x \neq 1
\\
2 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-b653f670fef69dcd7eda155255107eec.png)
no es continua en el punto
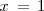 porque
porque
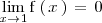 mientras que
mientras que
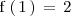 , es decir:
, es decir:
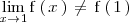
Como
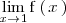 existe, la discontinuidad que
existe, la discontinuidad que
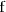 tiene en el punto
tiene en el punto
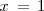 es evitable.
es evitable.
Una función presenta una discontinuidad de primera especie en el punto
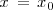 si los limites laterales de
si los limites laterales de
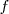 en
en
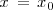 existen pero son distintos, es decir:
existen pero son distintos, es decir:
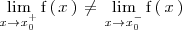
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-b4e00ff82dd6d614ad2d9cc1fc106612.png)
no es continua en el punto
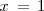 porque
porque
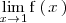 no existe, al ser ambos limites laterales distintos:
no existe, al ser ambos limites laterales distintos:
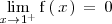

Como ambos limites laterales existen la discontinuidad que
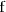 tiene en el punto
tiene en el punto
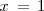 es de primera especie.
es de primera especie.
Una función
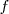 presenta una discontinuidad de segunda especie en el punto
presenta una discontinuidad de segunda especie en el punto
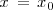 si no existe alguno de los limites laterales de
si no existe alguno de los limites laterales de
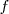 en dicho punto.
en dicho punto.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x
\\
1 & , & \quad \makebox{si} \quad x \, > \, 0
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x
\\
1 & , & \quad \makebox{si} \quad x \, > \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-d50a20a5903b019c747f584dde612451.png)
no es continua en el punto
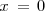 porque
porque
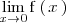 no existe, al no existir el limite por la izquierda de
no existe, al no existir el limite por la izquierda de
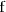 cuando
cuando
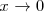 :
:
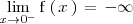
Como este limite por la izquierda no existe
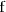 tiene en el punto
tiene en el punto
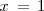 una discontinuidad de segunda especie.
una discontinuidad de segunda especie.



