Ángulo doble y ángulo mitad
De Wikillerato
(Diferencias entre revisiones)
| Línea 63: | Línea 63: | ||
\, - \, | \, - \, | ||
\left( | \left( | ||
| - | \, 1 \, - \, \mathrm{cos} | + | \, 1 \, - \, \mathrm{cos}^2 |
\left( | \left( | ||
| - | + | \, \alpha \, | |
| - | \right) | + | \right) |
| - | + | \right) | |
| - | \right) | + | \, = \, 2 \cdot \mathrm{cos}^2 |
| - | \, = \, 2 \cdot \mathrm{cos}^2 | + | \left( |
| - | \left( | + | \, \alpha \, |
| - | + | ||
\right) | \right) | ||
\right) | \right) | ||
Revisión de 14:44 10 ene 2007
Como se explica en la sección sobre las razones trigonométricas de la suma y diferencia de ángulos:
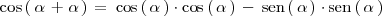
Teniendo en cuenta que
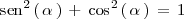 , deducimos que:
, deducimos que:
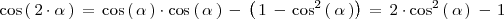
Según lo que se explica en la sección sobre razones trigonométricas de la suma y diferencia de ángulos:
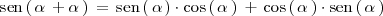
Por tanto
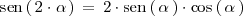
Si en las dos igualdades obtenidas:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{cos} \left( \, 2 \alpha \, \right) \, & = & \, 2 \cdot
\mathrm{cos}^2 \left( \, \alpha \, \right) \, - \, 1
\\
& &
\\
\mathrm{sen} \left( \, 2 \alpha \, \right) \, & = & \, 2 \cdot \mathrm{sen}
\left( \, \alpha \, \right) \cdot \mathrm{cos} \left( \, \alpha \, \right)
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{cos} \left( \, 2 \alpha \, \right) \, & = & \, 2 \cdot
\mathrm{cos}^2 \left( \, \alpha \, \right) \, - \, 1
\\
& &
\\
\mathrm{sen} \left( \, 2 \alpha \, \right) \, & = & \, 2 \cdot \mathrm{sen}
\left( \, \alpha \, \right) \cdot \mathrm{cos} \left( \, \alpha \, \right)
\end{array}
</pre>
<p>\right.](/images/math/math-47a3991f343b463fc7f3144fc2aee9a8.png)
sustituimos
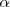 por
por
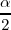 , obtenemos:
, obtenemos:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{cos} \left( \, \alpha \, \right) \, & = & \, 2 \cdot \mathrm{cos}^2
\left(
\, \frac{\alpha}{2} \,
\right)
\right)
\, - \, 1
\\
& &
\\
\mathrm{sen} \left( \, \alpha \, \right) \, & = & \, 2 \cdot
\mathrm{sen}
\left(
\, \frac{\alpha}{2} \,
\right)
\cdot \mathrm{cos}
\left(
\, \frac{\alpha}{2} \,
\right)
</pre>
<p>\end{array}
\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\mathrm{cos} \left( \, \alpha \, \right) \, & = & \, 2 \cdot \mathrm{cos}^2
\left(
\, \frac{\alpha}{2} \,
\right)
\right)
\, - \, 1
\\
& &
\\
\mathrm{sen} \left( \, \alpha \, \right) \, & = & \, 2 \cdot
\mathrm{sen}
\left(
\, \frac{\alpha}{2} \,
\right)
\cdot \mathrm{cos}
\left(
\, \frac{\alpha}{2} \,
\right)
</pre>
<p>\end{array}
\right.](/images/math/math-4f1fd31eefb8f6e79683f34e58743c08.png)
Si consideramos el anterior par de igualdades como un sistema de ecuaciones cuyas
incognitas son
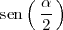 y
y
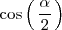 y resolvemos ese sistema de ecuaciones, se llega a las siguientes igualdades:
y resolvemos ese sistema de ecuaciones, se llega a las siguientes igualdades:
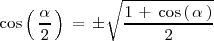
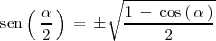
En ambos casos se elige el signo de la raiz en función de en que cuadrante este
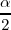 .
.



