Velocidad de propagación de una onda
De Wikillerato
Todas las ondas tienen una velocidad de propagación finita., en cuyo valor influyen las fuerzas recuperadoras elásticas del medio y determinados factores de la masa del medio: la densidad lineal en las cuerdas; la profundidad del agua bajo la superficie, o el coeficiente adiabático, la masa molecular y la temperatura en el caso de la propagación del sonido en un gas.
En todos los casos la velocidad es constante y, como siempre, será:
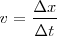
Pero veamos qué es el 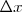 que la onda recorre en un tiempo
que la onda recorre en un tiempo 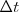 .
.
El periodo 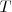 será el tiempo que transcurre entre dos instantes consecutivos en los cuales un punto del medio vuelve a poseer las mismas propiedades. Será pues igual
será el tiempo que transcurre entre dos instantes consecutivos en los cuales un punto del medio vuelve a poseer las mismas propiedades. Será pues igual 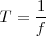 siendo
siendo 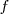 la frecuencia del movimiento oscilatorio del punto.
la frecuencia del movimiento oscilatorio del punto.
Por su parte el espacio recorrido por la onda en ese tiempo 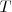 será la distancia entre dos puntos consecutivos que se encuentran con la misma propiedad. A esa distancia se le llama longitud de onda,
será la distancia entre dos puntos consecutivos que se encuentran con la misma propiedad. A esa distancia se le llama longitud de onda, 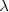 .
.
Por lo tanto 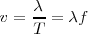
No obstante, esa velocidad puede medirse en algunos casos. Así:
a) Velocidad a lo largo de una cuerda Podrá realizarse midiendo el tiempo que tarda un pulso en llegar desde un punto A hasta otro B de la cuerda.
La ecuación que, de un modo general, nos permite determinar la velocidad en una cuerda es
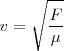
Donde 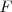 es la tensión a la que se encuentra sometida la cuerda. En la experiencia descrita es el peso de la masa
es la tensión a la que se encuentra sometida la cuerda. En la experiencia descrita es el peso de la masa 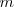 , es decir,
, es decir, 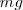 .
.
b) Velocidad en la superficie de un líquido
Con una cubeta de ondas medimos la distancia entre dos máximos consecutivos que se mantienen aparentemente inmóviles (ver experiencia de la cubeta de ondas). Conocida la frecuencia del estroboscopio se determina la velocidad con bastante precisión.
Véase la experiencia con la cubeta de ondas
c) Velocidad de las ondas sonoras
Con un generador de baja frecuencia y un altavoz podemos producir sonido. Con micrófono recibirlo. Si conectamos los bornes que salen del generador a una de las vías, la A por ejemplo, de un osciloscopio, en éste, observaremos las ondas emitidas. Si conectamos los bornes del altavoz a la otra vía del osciloscopio, la B, observaremos una onda de la misma longitud de onda y frecuencia, pero de diferente Amplitud, consecuencia de que la energía que emite el altavoz se tiene que repartir entre todos los puntos del espacio que se encuentren, con relación al altavoz, a la misma distancia que el micrófono.
Colocamos el micrófono a una distancia del altavoz tal que los valles de la onda que se observa en A coincida con las crestas de la onda que aparece en B.
Alejamos el altavoz siguiendo una regla que hemos colocado en la mesa de experimentación. Se observa que la onda de la vía B se va desplazando con relación a la onda de la vía A, al mismo tiempo que pierde amplitud. Llegamos a una situación en la cual las crestas de la vía A y de la vía B coinciden. La distancia recorrida por el altavoz es  . Si tomamos nota de la frecuencia emitida por el generador de baja frecuencia, podremos calcular la velocidad del sonido en el aire en esas condiciones de presión y temperatura.
. Si tomamos nota de la frecuencia emitida por el generador de baja frecuencia, podremos calcular la velocidad del sonido en el aire en esas condiciones de presión y temperatura.
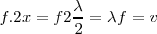
No obstante, siempre se puede medir como hizo Galileo. Desde un punto situado a una distancia conocida del lugar donde nos encontramos en el campo, se puede ver un fogonazo resultado de una explosión, el ruido de la explosión no nos llega hasta pasado unos segundos. Obtener v es sencillo. De hecho en los fuegos artificiales es fácil observarlo, pues hoy los cohetes alcanzan una altura notable.
De un modo general, la velocidad del sonido en un gas es:
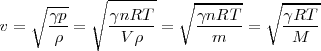
Donde 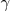 es el coeficiente adiabático de un gas, que depende de si las moléculas de la sustancia son monoatómicas (caso de un gas noble), biatómicas (caso del aire) o triatómicas (caso del dióxido de carbono).
es el coeficiente adiabático de un gas, que depende de si las moléculas de la sustancia son monoatómicas (caso de un gas noble), biatómicas (caso del aire) o triatómicas (caso del dióxido de carbono).
Para el aire 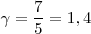
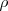 es la densidad del gas,
es la densidad del gas, 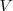 su volumen,
su volumen, 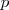 su presión y
su presión y 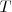 la temperatura,
la temperatura, 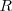 la constante de los gases,
la constante de los gases, 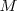 la masa molecular (para el aire 28,89),
la masa molecular (para el aire 28,89), 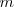 su masa y
su masa y  el número de moles.
el número de moles.
Dado que 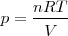 ,
, 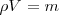 y
y 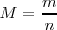 , se obtiene la forma última de expresar la ecuación
, se obtiene la forma última de expresar la ecuación
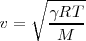
d) Para medir la velocidad de la luz son necesarios aparatos y procedimientos más sofisticados que exceden los estudios de bachillerato. En el vacío es:
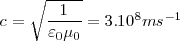
Donde 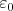 es la constante dieléctrica del vacío o permitividad y
es la constante dieléctrica del vacío o permitividad y 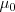 es la permeabilidad magnética del vacío.
es la permeabilidad magnética del vacío.
Conclusión
- - La velocidad es independiente de la forma y de energía (nos viene dada por la amplitud, A) que transporta la onda.
- Así, el sonido emitido por cualquier instrumento musical, independientemente de la amplitud del sonido, se propagan a ala misma velocidad en el aire, de otro modo no sería posible la formación de orquestas sinfónicas. Ni de cuerda, etc
- - Sin embargo, la velocidad depende de la naturaleza del medio y de su estado. Por ejemplo, la elasticidad del medio y su inercia tienen mucha importancia en el valor que adquiere la velocidad.



