Puntos de corte con los ejes de coordenadas

De Wikillerato

Tabla de contenidos

1 Introducción
2 Ejemplo
3 Puntos de corte con el eje X
4 Ejemplo
5 Punto de corte con el eje Y
6 Ejemplo

Introducción

La intersección de uno o mas conjuntos de puntos es el conjunto de puntos comunes, es decir, el conjunto de puntos que se encuentran en todos y cada uno de dichos conjuntos.

Es habitual encontrarse con que un conjunto de puntos se determina dando una propiedad que cumplen todos los puntos de dicho conjunto y solo ellos.

Por ejemplo, el eje X es el siguiente conjunto de puntos:

$\left\{ \left( \, x, \, y \, \right) \, \left| \, y = 0 \, \right. <pre>\right\} </pre> $

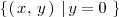
En este caso, 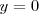$y = 0$ es la ecuación del eje X. El satisfacer esta igualdad es la propiedad que verifican todos los puntos del eje X y solo ellos.

Si queremos encontrar la intersección de varios conjuntos de puntos, cada uno de ellos caracterizados por una serie de ecuaciones, lo que haremos es juntar todas esas ecuaciones y formar un sistema de ecuaciones que resolveremos para encontrar los puntos comunes a todos esos conjuntos.

Ejemplo

Supongamos que queremos encontrar la intersección de la circunferencia de ecuación

$x^2 + y^2 = 4$

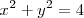
con la recta

$y = 3x + 1$

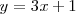
Para encontrar la intersección de ambas conjuntos de puntos ( la circunferencia y la recta ) juntamos las ecuaciones de ambos conjuntos para formar un sistema de ecuaciones

$\left\{ <pre> \begin{array}{l} y = 3x + 1 \\ x^2 + y^2 = 4 \end{array} </pre> \right.$

y lo resolvemos.

Puntos de corte con el eje X

Asi, para hallar los puntos de corte del eje X con la grafica de la función $\mathrm{f}$ , lo que haremos sera formar un sistema de ecuaciones con la ecuación del eje X y la ecuación de la gráfica del eje X

$\left\{ <pre> \begin{array}{l} y = 0 \\ y = \mathrm{f} \left( \, x \, \right) \end{array} </pre> \right.$

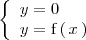
y resolver este sistema de ecuaciones con dos incognitas mediante igualación, es decir, mediante la resolución de la ecuación:

$\mathrm{f} \left( \, x \, \right) = 0$

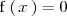
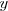Esta ecuación puede tener cero, una, varias o infinitas soluciones. Cada solución va a ser la coordenada $x$ ( abcisa ) de un punto de corte con el eje X. La coordena $y$ ( ordenada ) de dicho punto es 0.

Ejemplo

Busquemos los puntos de corte de la grafica de la función 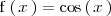$\mathrm{f} \left( \, x \, \right) = \cos \left( \, x \, \right)$ con el eje X.

Para ello, resolvemos el sistema de ecuaciones

$\left\{ <pre> \begin{array}{l} y = 0 \\ y = \cos \left( \, x \, \right) \end{array} </pre> \right.$

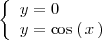
Por igualación, se tiene que <center> $\cos \left( \, x \, \right) = 0$

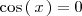
Esta ecuación tiene infintas soluciones

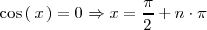$\cos \left( \, x \, \right) = 0 \Rightarrow x = \frac{\pi}{2} + n \cdot \pi$ con $n \in \mathbb{Z}$

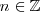
Por lo tanto, los puntos de corte de la gráfica de la función 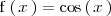$\mathrm{f} \left( \, x \, \right) = \cos \left( \, x \, \right)$ con el eje X son

$\ldots, \, \left( <pre> \, \frac{\pi}{2} -3 \cdot \pi, \, 0 \, </pre> \right) <pre>, \, </pre> \left( <pre> \, \frac{\pi}{2} -2 \cdot \pi, \, 0 \, </pre> \right) , \, \left( <pre> \, \frac{\pi}{2} - 1 \cdot \pi, \, 0 \, </pre> \right) , \, \left( <pre> \, \frac{\pi}{2} + 0 \cdot \pi, \, 0 \, </pre> \right) , \, \left( <pre> \, \frac{\pi}{2} + 1 \cdot \pi, \, 0 \, </pre> \right) , \, \left( <pre> \, \frac{\pi}{2} + 2 \cdot \pi, \, 0 \, </pre> \right) , \, \left( <pre> \, \frac{\pi}{2} + 3 \cdot \pi, \, 0 \, </pre> \right) , \, \ldots$

Punto de corte con el eje Y

Para hallar los puntos de corte del eje Y con la grafica de la función $\mathrm{f}$ procedemos de una manera análoga.

Formamos un sistema de ecuaciones con la ecuación del eje X y la ecuaci\'on de la gr\'afica del eje Y ( 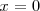$x = 0$ ) y resolveremos dicho sistema:

$\left\{ <pre> \begin{array}{l} x = 0 \\ y = \mathrm{f} \left( \, x \, \right) \end{array} </pre> \right.$

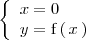
Este sistema de ecuaciones con dos incognitas se resuelve por sustitución y su solución es unica:

$\left( \, x, \, y \, \right) = \left( \, 0, \, \mathrm{f} \left( \, 0 \, \right)$

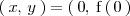
Ejemplo

Busquemos el punto de corte de la grafica de la función 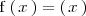$\mathrm{f} \left( \, x \, \right) = \corrects \left( \, x \, \right)$ con el eje Y.

Para ello, resolvemos el sistema de ecuaciones

$\left\{ <pre> \begin{array}{l} x = 0 \\ y = \cos \left( \, x \, \right) \end{array} </pre> \right.$

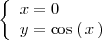
Por sustitución, se tiene que

$y = \cos \left( \, 0 \, \right) = 1$

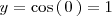
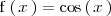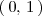Por lo tanto, el punto de corte de la gráfica de la función $\mathrm{f} \left( \, x \, \right) = \cos \left( \, x \, \right)$ con el eje Y es el punto $\left( <pre> \, 0, \, 1 \, </pre> \right)$ .