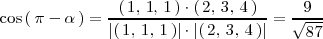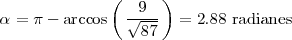Problemas de ángulos
De Wikillerato
Tabla de contenidos |
Ángulo entre dos rectas
El ángulo entre dos rectas
 y
y
 del espacio es el menor angulo entre las rectas que se obtienen al proyectar
del espacio es el menor angulo entre las rectas que se obtienen al proyectar
 y
y
 en un mismo plano paralelo a ambas rectas.
Las rectas se proyectan en un mismo plano porque, en general,
no tienen porque encontrarse en un mismo plano ( no tienen porque ser
coplanarias ).
en un mismo plano paralelo a ambas rectas.
Las rectas se proyectan en un mismo plano porque, en general,
no tienen porque encontrarse en un mismo plano ( no tienen porque ser
coplanarias ).
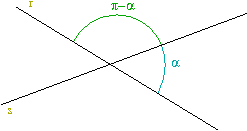
Dos rectas en el plano forman dos angulos, uno menor, llamemoslos, por ejemplo,
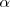 ,
y otro mayor ( o igual ), que seria el suplementario de
,
y otro mayor ( o igual ), que seria el suplementario de
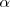 ,
,
 .
.
El ángulo entre dos rectas
 y
y
 cuyos vectores directores son, respectivamente,
cuyos vectores directores son, respectivamente,
 y
y
 ,
se puede calcular con la siguiente fórmula:
,
se puede calcular con la siguiente fórmula:
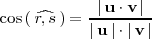
Calculando el arcocoseno del resultado obtenido aplicando la fórmula anterior se
obtiene el ángulo que forman las retas
 y
y
 .
.
En la fórmula anterior
 denota el producto escalar de los vectores
denota el producto escalar de los vectores
 y
y
 .
.
Ejemplo
Calculemos el ángulo entre las rectas de ecuaciones
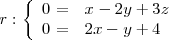
y
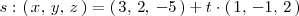
La recta
 viene dada como la intersección de dos planos ( el plano
viene dada como la intersección de dos planos ( el plano
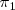 de ecuación
de ecuación
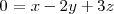 y el plano
y el plano
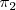 de ecuación
de ecuación
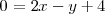 ).
).
Un vector director
 de la recta
de la recta
 es el vector que multiplica al parametro
es el vector que multiplica al parametro
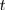 en su ecuación, es decir:
en su ecuación, es decir:
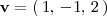
Podemos obtener un vector director
 de la recta
de la recta
 multiplicando vectorialmente un vector perpendicular al plano
multiplicando vectorialmente un vector perpendicular al plano
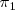 por un vector perpendicular al plano
por un vector perpendicular al plano
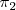 .
.
Un vector
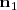 perpendicular al plano
perpendicular al plano
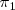 lo podemos obtener de los coeficientes de x, y, z en la ecuación de
lo podemos obtener de los coeficientes de x, y, z en la ecuación de
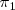 :
:
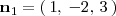
De la misma forma obtenemos un vector
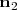 perpendicular al plano
perpendicular al plano
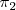 :
:
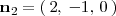
El producto vectorial de ambos vectores,
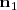 y
y
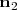 es
es

donde
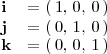
El ángulo que forman las rectas
 y
y
 es, por tanto
es, por tanto
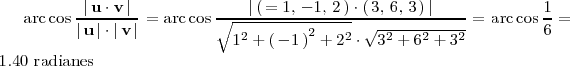
Ángulo entre dos planos
El ángulo que forman dos planos
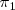 y
y
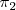 cuyos vectores normales son, respectivamente,
cuyos vectores normales son, respectivamente,
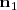 y
y
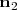 es igual al ángulo que forman
es igual al ángulo que forman 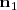 y
y
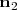 , que se puede hallar calculando el arcocoseno de
, que se puede hallar calculando el arcocoseno de
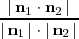
Ejemplo
Calculemos el ángulo entre los planos de ecuaciones:
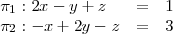
Sus vectores normales son, respectivamente:
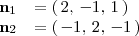
Así
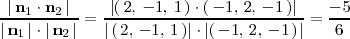
Por lo tanto, el ángulo que forman ambos planos es
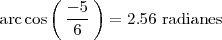
Ángulo entre una recta y un plano
El ángulo
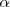 que forma una recta
que forma una recta
 cuyo vector director es
cuyo vector director es
 y un plano
y un plano
 cuyo ángulo normal es
cuyo ángulo normal es
 es complementario al ángulo que forman
es complementario al ángulo que forman
 y
y
 .
.
Por lo tanto, se tiene que
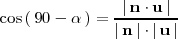
Ejemplo
Calculemos el ángulo
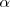 entre el plano
entre el plano
 de ecuación:
de ecuación:
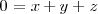
y la recta
 de ecuación:
de ecuación:
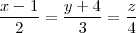
Un vector director de
 es
es
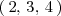 y un vector normal de
y un vector normal de
 es
es
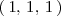 ,
por lo tanto:
,
por lo tanto: