Estroboscopio
De Wikillerato
Un estroboscopio es un aparato que emite centelleos con una frecuencia regulable. Es el aparato que suele usarse en las discotecas para ver bailar a la gente en diferentes posiciones fijas.
Su funcionamiento es comparable al de un flash electrónico.
Se pueden obtener centelleos de una cadencia regular con un procedimiento sencillo.
Si situamos una lámpara incandescente a una distancia igual al doble de la distancia focal de una lente convergente, los rayos atraviesan la lente y, al salir, se juntan en el centro imagen. En este centro imagen de la lente, se coloca un disco al que se le han practicado orificios equidistantes. El disco puede girar con velocidad angular constante alrededor de un eje, perpendicular a su plano y que pasa por el centro del círculo, movido por un motor de frecuencia N, de modo que del otro lado del disco aparecerán ráfagas de luz intermitentes con una cadencia uniforme.
La frecuencia de los centelleos será 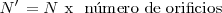
En este caso, 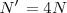
Cada orificio tarda un periodo 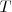 , siendo
, siendo 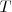 el periodo de su movimiento circular.
el periodo de su movimiento circular.
Pero si hay 4 orificios equidistantes, el periodo de los centelleos 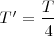 , con lo cual:
, con lo cual: 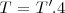
No obstante, los discos más frecuentemente usados son los de un solo orificio, tal y como veremos en la cubeta de ondas.
Si el disco posee un solo orificio la frecuencia de las ráfagas de luz coincidirá con la del motor, de tal modo que si el motor diese 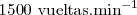 , la frecuencia de centelleo será:
, la frecuencia de centelleo será:
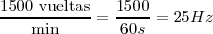
Es evidente que si el disco tuviese 6 orificios equidistantes, la frecuencia de los centelleos sería de 150 Hz.
Determinación de la frecuencia de un móvil
a) Péndulo
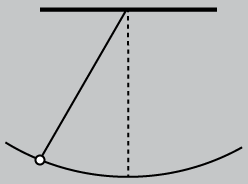
El procedimiento es muy simple. Se pone el péndulo en movimiento, oscilando alrededor de la posición de equlibrio, Se regula el estroboscopio de modo que vemos las posiciones del péndulo cada vez más espaciadas, hasta que llega un momento en que la frecuencia 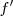 del estroboscopio coincide con la frecuencia
del estroboscopio coincide con la frecuencia 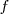 del péndulo:
del péndulo:
En este caso veremos al péndulo inmóvil en una sola posición.
.Si el periodo de centelleo es la mitad del periodo del péndulo, su frecuencia de centelleo del estroboscopio 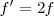 . Y podremos ver sólo las posiciones extremas o sólo la de equilibrio.
. Y podremos ver sólo las posiciones extremas o sólo la de equilibrio.
En el caso de que el estroboscopio tuviera cuatro orificios, como el que se ha presentado, el péndulo podría aparecer inmóvil en cuatro posiciones, pero en ciertos casos podrían ser sólo dos o tres posiciones.
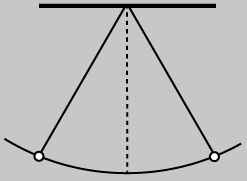
Si el péndulo es iluminado cuando se encuentra en el equilibrio o en uno de los de máxima elongación, sólo veremos tres posiciones: las de los extremos y la posición de equilibrio que es iluminada dos veces, tanto al moverse hacia la izquierda como hacia la derecha:
Si el comienzo de los centelleos coincide con una posición tal, que el tiempo que tarda en volver a la misma posición es  , veremos sólo dos posiciones, más cercanas a los extremos, van a menos velocidad, que a la posición de equilibrio.
, veremos sólo dos posiciones, más cercanas a los extremos, van a menos velocidad, que a la posición de equilibrio.
¿Qué ocurre si el estroboscopio poseyera seis orificios?
Si regulamos la frecuencia del estroboscopio de modo que sólo veamos una posición ( no la del equilibrio) la frecuencia del centelleo será igual a la del péndulo. La pregunta que podría hacerse es por qué no nos sirve la posición del equilibrio.
b) Disco blanco con un radio pintado de negro con movimiento circular uniforme
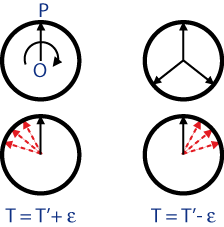
El disco gira alrededor de un eje fijo en tanto lo iluminamos con el estroboscopio. La posición del radio vertical 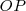 nos servirá de referencia.
nos servirá de referencia.
Supongamos que la frecuencia de rotación del disco sea 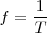 y que la frecuencia del estroboscopio fuese
y que la frecuencia del estroboscopio fuese 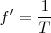 . El tiempo que transcurre entre dos centelleos es pues
. El tiempo que transcurre entre dos centelleos es pues 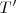 .
.
Veamos que casos pueden suceder:
a) El radio marcado aparece inmóvil. Esto quiere decir que 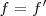 , es decir, el disco describe un círculo completo entre dos centelleos.
, es decir, el disco describe un círculo completo entre dos centelleos.
b) El radio del disco aparece en tres posiciones diferentes. Esto quiere decir que el disco ha descrito un tercio de círculo entre dos centelleos, o lo que es igual, el periodo del estroboscopio es 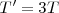 , y por lo tanto
, y por lo tanto 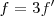
c) Pero puede suceder que el periodo del disco 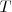 sea aproximadamente igual periodo del estroboscopio, es decir
sea aproximadamente igual periodo del estroboscopio, es decir 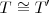 , es decir
, es decir 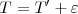 o también
o también 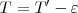
En el primer caso, 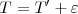 , el periodo del disco es algo mayor que el del estroboscopio. Cuando éste ilumina, la flecha aún no ha descrito un círculo, aparentemente se mueve hacia atrás.
, el periodo del disco es algo mayor que el del estroboscopio. Cuando éste ilumina, la flecha aún no ha descrito un círculo, aparentemente se mueve hacia atrás.
En el segundo caso, 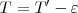 , el periodo del estroboscopio es algo más largo que el del disco. La flecha describe algo más de un círculo entre dos centelleos consecutivos. Parece que se mueve hacia delante.
, el periodo del estroboscopio es algo más largo que el del disco. La flecha describe algo más de un círculo entre dos centelleos consecutivos. Parece que se mueve hacia delante.
En el primer caso, el radio que se ha pintado sobre el disco, no describe un círculo completo, sino 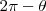 . El ángulo descrito hacia atrás, en un periodo del estroboscopio, es:
. El ángulo descrito hacia atrás, en un periodo del estroboscopio, es:
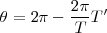
Pues 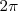 es el ángulo que hubiera descrito el círculo si su periodo hubiese sido igual al del osciloscopio, y
es el ángulo que hubiera descrito el círculo si su periodo hubiese sido igual al del osciloscopio, y 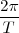 es la velocidad angular del disco por el tiempo
es la velocidad angular del disco por el tiempo 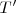 transcurrido.
transcurrido.
Pero veamos cómo se puede calcular la velocidad aparente de la flecha, el periodo aparente del disco y su frecuencia.
Es decir, la velocidad angular con que se mueve la flecha es: 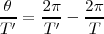 con lo cual
con lo cual 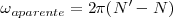 .
.
Pero la velocidad angular aparente es:
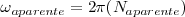
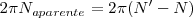
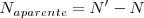
En el segundo caso, el disco ha descrito un poco más de un círculo, la flecha tiene un movimiento aparente hacia delante
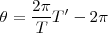
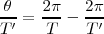
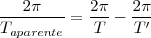
Cancelando 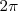 y sustituyendo los periodos por las frecuencias
y sustituyendo los periodos por las frecuencias
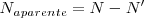
Donde 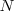 es la frecuencia del disco y
es la frecuencia del disco y 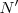 la del estroboscopio.
la del estroboscopio.
Como ya se verá en la rotación de los satélites artificiales, estas relaciones son de una gran utilidad.
Tweet