Bisectriz de un ángulo
De Wikillerato
La bisectriz de un ángulo formado por dos rectas r y s que se cortan en el punto V se define como el lugar geométrico de los puntos del plano que están a la misma distancia de la recta r que de la recta s. La bisectriz de un ángulo es otra recta concurrente con las dos que forman el ángulo, es decir, que pasa también por el vértice V del ángulo.
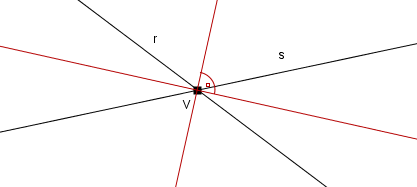
Evidentemente, dos rectas r y s que se cortan dividen al plano en cuatro regiones y forman igualmente cuatro ángulos distintos con el mismo vértice. De estos cuatro ángulos los que son opuestos por el vértice son iguales entre sí y los adyacentes son complementarios. Los ángulos opuestos por el vértice comparten la misma bisectriz, mientras que las bisectrices de dos ángulos complementarios adyacentes son ortogonales (perpendiculares).
Para determinar la bisectriz del ángulo determinado por dos semirectas r y s con origen en un vértice común V habrá que determinar primero un punto P que equidiste de las dos semirectas. Una vez determinado éste, la semirecta con origen en V que pasa por el punto P será la bisectriz buscada.
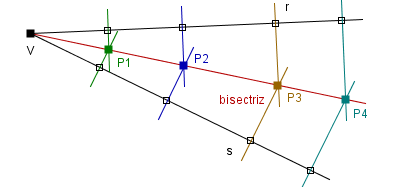
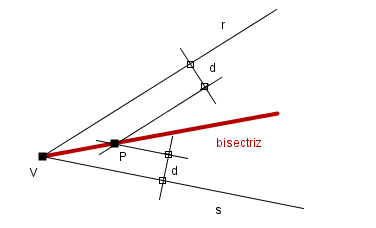
Una posibilidad es trazar una recta paralela a r a una distancia d de la misma, y otra recta paralela a s que esté a la misma distancia d de ella. Ambas paralelas se cortarán en un punto P, que equidista de r y s, siendo por lo tanto la recta VP la bisectriz del ángulo formado por r y s.
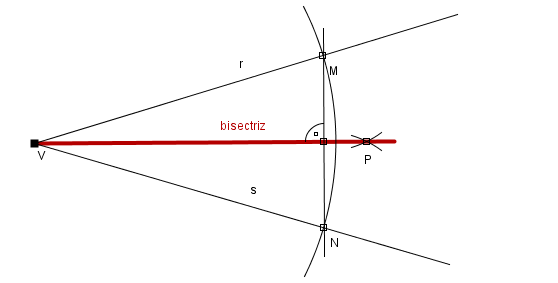
Dados un punto M sobre la recta r y otro punto N sobre la recta s, ambos a la misma distancia del vértice V, la bisectriz del ángulo formado por las rectas r y s coincidirá con la mediatriz del segmento MN, lo que nos brinda una construcción alternativa de la bisectriz de un ángulo.
Cuando el vértice del ángulo no es accesible (está fuera de los límites del papel) se dibuja una recta cualquiera que atraviese a las dos dadas. Se dibujan las bisectrices de los cuatro ángulos que se forman entre las dos rectas dadas y la auxiliar. Uniendo los puntos de corte de las cuatro bisectrices se obtiene la bisectriz de las dos rectas dadas.