Aplicaciones del teorema de Tales
De Wikillerato
Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la cuarta y tercera proporcional de dos segmentos dados, la media proporcional, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones.
Tabla de contenidos |
División de un segmento en partes proporcionales
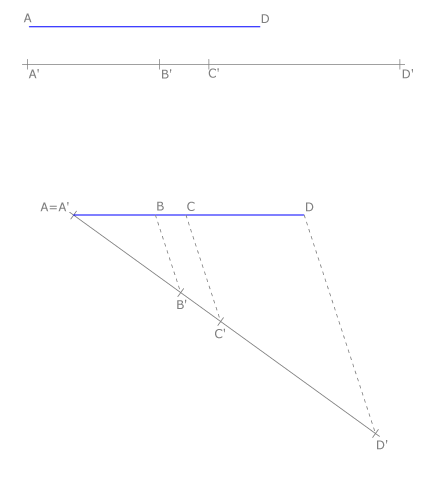
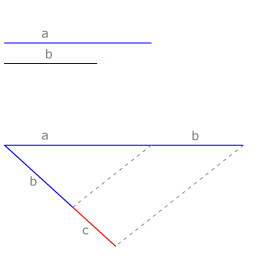
Para dividir un segmento AD en partes proporcionales a las partes A’B’, B’C’ y C’D’ dadas, trazamos una recta que pase por A definiendo así un haz de dos rectas. Sobre ella llevamos las magnitudes dadas. Por el extremo D’ trazamos la recta DD’ . Trazamos paralelas a DD’ por los puntos B’ y C’ .
Estas paralelas cortan al segmento dado en los puntos B y C.
Por el teorema de Tales, se cumplirá que 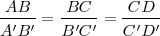 .
.
División de un segmento en partes iguales.
Para dividir un segmento AB dado en n partes iguales, trazamos una recta que pase por A. Situamos sobre ella con el compas, n partes iguales, numeramos. En este caso n=9. Dibujamos la recta 9B y trazamos paralelas a ella por los puntos restantes, ordenadamente.
Por ser equidistantes las paralelas los segmentos definidos sobre AB son igual
Demostración del teorema de la bisectriz
La bisectriz del ángulo BAC de un triángulo ABC divide a su lado opuesto en partes proporcionales a los otros lados del triángulo.
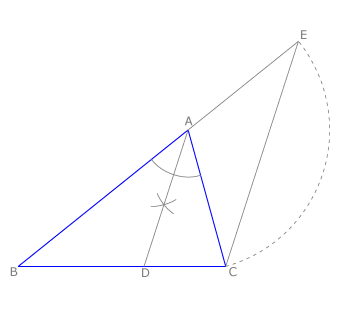
Consideramos el triángulo ABC y su bisectriz AD.
Según el teorema:
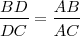
Vamos a comprobarlo:
Trazamos por C una paralela a AD, que corta a la prolongación de AB en E.
Por el teorema de Tales, se cumple que:
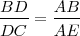
Los ángulos BAD=AEC por tener un lado común y los otros paralelos entre sí y DAC=ACE por ser alternos internos.
Como BAD = DAC tenemos que AEC = ACE, lo que indica que el triángulo ACE es isósceles con base EC, luego AC = AE.
Lo aplicamos a la igualdad anterior y resulta que
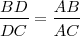
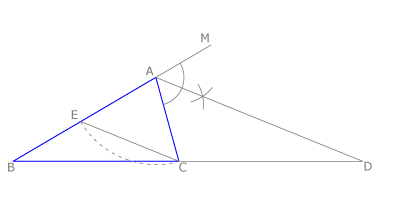
El mismo razonamiento vale si consideramos la bisectriz del ángulo exterior MAC.
Cuarta proporcional de tres segmentos
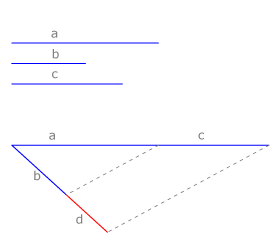
Dados tres segmentos a, b y c, se llama magnitud cuarta proporcional de ellos a un segmento d que verifica: a/b=c/d.
Para hallarlo aplicamos el teorema de Tales: dibujamos un haz de dos rectas. Sobre una de las rectas situamos los segmentos a y c y sobre la otra el segmento b, como se ve en la figura.
Trazamos la recta que une los extremos de a y b y trazamos una paralela por el extremo de c. Esta paralela define el segmento d solución del problema, pues: a/b=c/d
Tercera proporcional de dos segmentos
Dados dos segmentos a y b, se llama magnitud tercera proporcional de ellos a un segmento c que verifica: a/b=b/c.
Vemos que es un caso particular de cuarta proporcional, con los términos intermedios iguales.
Para hallarlo aplicamos el teorema de Tales: dibujamos un haz de dos rectas. Sobre una de las rectas situamos los segmentos a y b y sobre la otra el segmento b, como se ve en la figura.
Trazamos la recta que une los extremos de a y b y trazamos una paralela por el extremo de b. Esta paralela define el segmento c solución del problema, pues: a/b=b/c
La proporción áurea
Cuando en una tercera proporcional el término mayor es igual a la suma de los otros dos se verifica que:
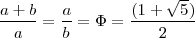
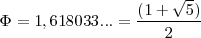 es el número de oro.
es el número de oro.
Cuando un rectángulo tiene los lados con esta proporción recibe el nombre de rectángulo de oro. En el capítulo dedicado a las relaciones del arte con la geometría veremos la importancia de 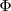 en el estudio de las proporciones armónicas. Más adelante estudiaremos las espirales relacionadas con el rectángulo de oro.
en el estudio de las proporciones armónicas. Más adelante estudiaremos las espirales relacionadas con el rectángulo de oro.
También es fundamental para la construcción del pentágono regular, pues la proporción áurea se cumple entre su diagonal y su lado:
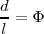
Vamos a comprobar que
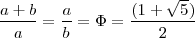
Operamos:
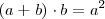
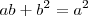
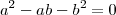
Resulta una ecuación de segundo grado donde la incógnita es a. Vamos a despejarla. Nos interesa sólo la raíz positiva:
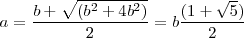
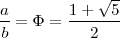
Vamos a construir segmentaciones áureas a partir de diferentes datos:
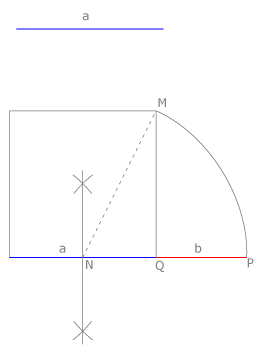
Cuando el dato es a
Dibujamos un cuadrado de lado a y la mediatriz de dicho lado. Con centro en N, punto medio de a, y radio NM, diagonal de medio cuadrado, trazamos un arco que corta en P a la prolongación de a, definiendo el segmento b. Se cumple que 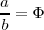
Vamos a comprobarlo:
Como 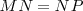 , pues son radios de la misma circunferencia, resulta que:
, pues son radios de la misma circunferencia, resulta que:
Consideramos el triángulo MNQ, por Pitágoras:
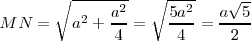
En nuestro dibujo:
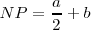
Lo aplicamos en la igualdad anterior:
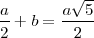
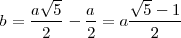
luego:
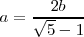
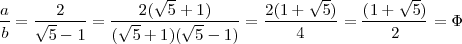
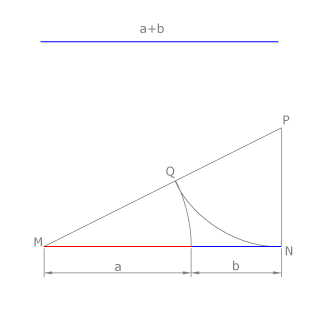
Cuando el dato es a+b
Ésta es otra construcción de la segmentación áurea. Sea MN= a+b. Trazamos un segmento perpendicular de magnitud MN/2 y dibujamos el triángulo rectángulo MNP. Con centro en P y radio PN trazamos un arco que corta a la hipotenusa en el punto Q. Con centro en A trazamos un arco de radio AQ que corta a MN en el punto R, definiendo los segmentos a y b.
Se verifica que: 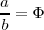
Vamos a comprobarlo:
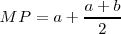 , ya que
, ya que
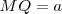 y
y 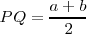
Considerando el triángulo MNP, por Pitágoras:
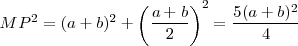 , luego:
, luego:
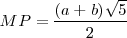
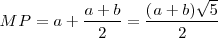
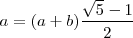
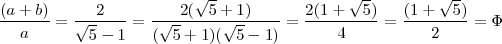
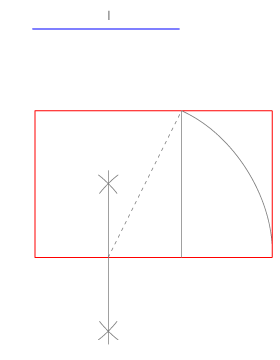
Los rectángulos de oro
Si el dato es el lado menor a usamos la primera construcción de segmentación áurea.
Si el dato es el lado mayor, a+b, utilizamos la segunda.