Proporcionalidad directa
De Wikillerato
(→Teorema de Tales) |
(→Aplicaciones del teorema de Tales) |
||
| Línea 35: | Línea 35: | ||
Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la tercera proporcional de dos segmentos dados, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones. | Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la tercera proporcional de dos segmentos dados, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones. | ||
| + | |||
| + | ====División de un segmento en partes proporcionales==== | ||
| + | |||
| + | Para dividir un segmento '''AD ''' en partes proporcionales a las partes '''A’B’, B’C’ y C’D’ ''' dadas, trazamos una recta que pase por '''A''' definiendo así un haz de dos rectas. Sobre ella llevamos las magnitudes dadas. Por el extremo '''D’ ''' trazamos la recta '''DD’ '''. Trazamos paralelas a '''DD’ ''' por los puntos '''B’''' y '''C’ '''. Estas paralelas cortan al segmento dado en los puntos '''B''' y '''C'''. | ||
| + | Por el teorema de Tales, se cumplirá que '''AB/A’B’=BC/B’C’=CD/C’D’'''. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 3.gif]] | ||
| + | |||
| + | ====División de un segmento en partes iguales. ==== | ||
| + | |||
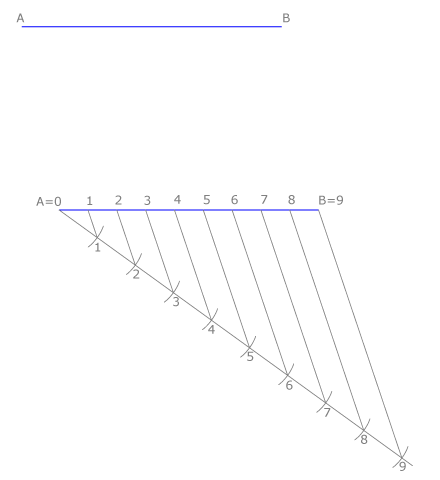
| + | Para dividir un segmento '''AB''' dado en '''n''' partes iguales, trazamos una recta que pase por '''A'''. | ||
| + | Situamos sobre ella '''n''' partes iguales, que numeramos. En este caso '''n=9'''. Dibujamos la recta '''9B''' y trazamos paralelas a ella por los puntos restantes, ordenadamente. | ||
| + | |||
| + | Por ser equidistantes las paralelas los segmentos definidos sobre '''AB''' son iguales. | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 4.gif]] | ||
| + | |||
| + | ====Demostración del teorema de la bisectriz==== | ||
| + | |||
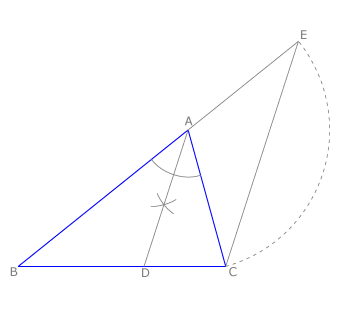
| + | La bisectriz del ángulo '''BAC''' de un triángulo '''ABC''' divide a su lado opuesto en partes proporcionales a los otros lados del triángulo. | ||
| + | Consideramos el triángulo '''ABC''' y su bisectriz '''AD'''. Según el teorema: '''BD/DC=AB/AC. ''' | ||
| + | |||
| + | Vamos a comprobarlo: | ||
| + | |||
| + | Trazamos por '''C''' una paralela a '''AD''', que corta a la prolongación de '''AB''' en '''E'''. | ||
| + | |||
| + | Por el teorema de Tales, se cumple que: '''BD/DC=AB/AE'''. | ||
| + | |||
| + | Los ángulos '''BAD=AEC''' por tener un lado común y los otros paralelos entre sí y '''DAC=ACE''' por ser alternos internos. | ||
| + | |||
| + | Como '''BAD=DAC''' tenemos que '''AEC=ACE''', lo que indica que el triángulo '''ACE''' es isósceles con base '''EC''', luego '''AC=AE'''. | ||
| + | |||
| + | Lo aplicamos a la igualdad anterior y resulta que '''BD/DC=AB/AC'''. | ||
| + | |||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 5.gif]] | ||
| + | |||
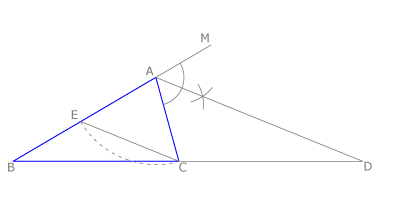
| + | El mismo razonamiento vale si consideramos la bisectriz del ángulo exterior '''MAC. ''' | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 6.gif]] | ||
| + | |||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión de 16:19 8 ene 2009
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Características generales
Consideramos que una variable  puede adquirir los valores [Unparseable or potentially dangerous latex formula. Error 3 ] y otra variable y los valores [Unparseable or potentially dangerous latex formula. Error 3 ]
puede adquirir los valores [Unparseable or potentially dangerous latex formula. Error 3 ] y otra variable y los valores [Unparseable or potentially dangerous latex formula. Error 3 ]  e
e 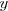 son directamente proporcionales si [Unparseable or potentially dangerous latex formula. Error 3 ]
son directamente proporcionales si [Unparseable or potentially dangerous latex formula. Error 3 ]
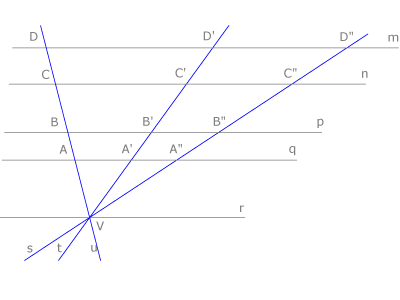
Teorema de Tales
Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: [Unparseable or potentially dangerous latex formula. Error 3 ] [Unparseable or potentially dangerous latex formula. Error 3 ]
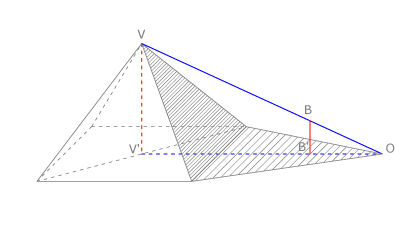
En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón 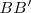 .
.
En nuestra figura vemos que la altura 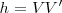 es la incógnita de esta igualdad: [Unparseable or potentially dangerous latex formula. Error 3 ], luego
es la incógnita de esta igualdad: [Unparseable or potentially dangerous latex formula. Error 3 ], luego
[Unparseable or potentially dangerous latex formula. Error 3 ]
El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que:
[Unparseable or potentially dangerous latex formula. Error 3 ]
[Unparseable or potentially dangerous latex formula. Error 3 ]
De la primera igualdad deducimos la segunda ya que:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Aplicaciones del teorema de Tales
Las aplicaciones del teorema de Tales son muchas y muy importantes: la división de un segmento en partes proporcionales, la división de un segmento en partes iguales, la tercera proporcional de dos segmentos dados, la segmentación áurea, la cuarta proporcional de tres segmentos dados, el cálculo gráfico de productos y razones de segmentos dados, el cálculo de razones simples, razones dobles y cuaternas armónicas, la semejanza y el estudio de las escalas. Todas estas construcciones son de gran interés para la resolución de problemas y para el estudio de las transformaciones.
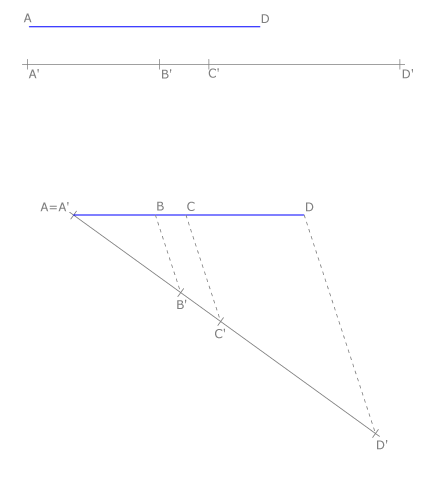
División de un segmento en partes proporcionales
Para dividir un segmento AD en partes proporcionales a las partes A’B’, B’C’ y C’D’ dadas, trazamos una recta que pase por A definiendo así un haz de dos rectas. Sobre ella llevamos las magnitudes dadas. Por el extremo D’ trazamos la recta DD’ . Trazamos paralelas a DD’ por los puntos B’ y C’ . Estas paralelas cortan al segmento dado en los puntos B y C. Por el teorema de Tales, se cumplirá que AB/A’B’=BC/B’C’=CD/C’D’.
División de un segmento en partes iguales.
Para dividir un segmento AB dado en n partes iguales, trazamos una recta que pase por A. Situamos sobre ella n partes iguales, que numeramos. En este caso n=9. Dibujamos la recta 9B y trazamos paralelas a ella por los puntos restantes, ordenadamente.
Por ser equidistantes las paralelas los segmentos definidos sobre AB son iguales.
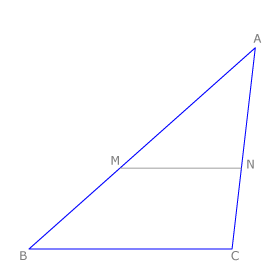
Demostración del teorema de la bisectriz
La bisectriz del ángulo BAC de un triángulo ABC divide a su lado opuesto en partes proporcionales a los otros lados del triángulo. Consideramos el triángulo ABC y su bisectriz AD. Según el teorema: BD/DC=AB/AC.
Vamos a comprobarlo:
Trazamos por C una paralela a AD, que corta a la prolongación de AB en E.
Por el teorema de Tales, se cumple que: BD/DC=AB/AE.
Los ángulos BAD=AEC por tener un lado común y los otros paralelos entre sí y DAC=ACE por ser alternos internos.
Como BAD=DAC tenemos que AEC=ACE, lo que indica que el triángulo ACE es isósceles con base EC, luego AC=AE.
Lo aplicamos a la igualdad anterior y resulta que BD/DC=AB/AC.
El mismo razonamiento vale si consideramos la bisectriz del ángulo exterior MAC.
Tweet