Métodos de resolución de sistemas de ecuaciones lineales
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | |||
| - | == | + | ==Introducción== |
<br/> | <br/> | ||
| - | + | Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones. | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Los métodos de [[Métodos de resolución de sistemas de ecuaciones lineales#Método de igualación|igualación]], [[Métodos de resolución de sistemas de ecuaciones lineales#Método de sustitución|sustitución]] y [[Métodos de resolución de sistemas de ecuaciones lineales#Método de reducción|reducción]] consisten en | ||
| + | encontrar y resolver, para cada una de las incognitas, una ecuación con esa | ||
| + | incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas | ||
| + | facil, ¿no?). | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | A estas ecuaciones, con solo una incognita, se llega a traves de una serie de | ||
| + | pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos | ||
| + | incognitas que las ecuaciones previas. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Así, es posible que en uno de estos pasos de eliminación de incognitas se utilize | ||
| + | un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se | ||
| + | utilize otro método ( el de igualación, por ejemplo ). | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Cada vez que se encuentra la solución para una incognita, se sustituye esta | ||
| + | incognita por su solución para obtener asi ecuaciones con menos incognitas. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar | ||
| + | para resolver [[Definición y tipos#Sistemas de ecuaciones lineales compatibles determinados|sistemas de ecuaciones compatibles determinados]] e | ||
| + | [[Definición y tipos#Sistemas de ecuaciones lineales compatibles indeterminados|indeterminados]]. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Estos mismos métodos tambien pueden utilizarse para comprobar si un sistema de | ||
| + | ecuaciones es compatible o no. La utilizacion de cualquiera de ellos | ||
| + | conduciria, en el caso de que el sistema fuese incompatible, a una igualdad que | ||
| + | es falsa, por ejemplo: | ||
| + | <center> | ||
<math> | <math> | ||
| - | + | 2 = 3 | |
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | <br/> | ||
| + | |||
| + | El [[Métodos de resolución de sistemas de ecuaciones lineales#Método de la matriz inversa|método de la matriz inversa]] y la [[Métodos de resolución de sistemas de ecuaciones lineales#Regla de Cramer|regla de Cramer]] solo se pueden utilizar en | ||
| + | el caso de que el sistema de ecuaciones lineales sea compatible determinado. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Método de reducción== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número | ||
| + | de incognitas hasta llegar a ecuaciones con solo una incognita. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de | ||
| + | la ecuación por dicho número. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho | ||
| + | ( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las | ||
| + | ecuaciones que se suman. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
<math> | <math> | ||
| - | + | \left\{ | |
| + | \begin{array}{l} | ||
| + | 5x - 3y = 2 | ||
| + | \\ | ||
| + | 3x - 4y = -1 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| + | \begin{array}{l} | ||
| + | 15x - 9y = 6 | ||
| + | \\ | ||
| + | -15x + 20y = 5 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| - | + | </center> | |
| + | |||
| + | El sumar ambas ecuaciones nos da la ecuación | ||
| + | <center> | ||
| + | <math> | ||
| + | 11y = 11 | ||
| + | </math> | ||
| + | </center> | ||
| + | que es una ecuación con una sola incognita y cuya solución es | ||
| + | <center> | ||
| + | <math> | ||
| + | y = 1 | ||
| + | </math> | ||
| + | </center> | ||
| + | La elección de los factores 3 y -5 se ha hecho precisamente para que la | ||
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | + | desaparezca al sumar ambas ecuaciones. | |
<br/> | <br/> | ||
| + | Sutituyendo <math> y </math> por uno en la primera ecuación del sistema de | ||
| + | ecuaciones de partida, se obtiene | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | 5x - 3 = 2 | |
</math> | </math> | ||
</center> | </center> | ||
| + | que es otra ecuación con una sola incognita y cuya solución es | ||
| + | <math> | ||
| + | x = 1 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ==Método de igualación== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | El método de igualación consiste en lo siguiente: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Supongamos que tenemos dos ecuaciones: | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| + | \begin{array}{l} | ||
| + | a = b | ||
| + | \\ | ||
| + | a = c | ||
| + | \item \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| - | + | </center> | |
| - | + | donde | |
<math> | <math> | ||
| - | + | a | |
| + | </math>, | ||
| + | <math> | ||
| + | b | ||
| + | </math>, | ||
| + | y | ||
| + | <math> | ||
| + | c | ||
</math> | </math> | ||
| - | . | + | representan simplemente los miembros de estas ecuaciones ( son expresiones |
| + | algebraicas ). | ||
<br/> | <br/> | ||
| - | = | + | De las dos igualdades anteriores se deduce que |
| + | <center> | ||
| + | <math> | ||
| + | b = c | ||
| + | </math> | ||
| + | </center> | ||
| + | Si resulta que una incognita del sistema de ecuaciones no aparece ni en | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | ni en | ||
| + | <math> | ||
| + | b | ||
| + | </math>, | ||
| + | entonces la ecuación | ||
| + | <center> | ||
| + | <math> | ||
| + | b = c | ||
| + | </math> | ||
| + | </center> | ||
| + | no contendría dicha incognita. | ||
<br/> | <br/> | ||
| - | + | Este proceso de eliminación de incognitas se puede repetir varias veces hasta | |
| - | + | llegar a una ecuación con solo una incognita, digamos | |
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | . | ||
<br/> | <br/> | ||
| - | Una | + | Una vez que se obtiene la solución de esta ecuación se sustituye |
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | por su solución en otras ecuaciones dode aparezca | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | para reducir el número de incognitas en dichas ecuaciones. | ||
<br/> | <br/> | ||
| - | + | ===Ejemplo=== | |
<br/> | <br/> | ||
| - | == | + | El sistema de ecuaciones |
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | 2x - 3y = -1 | ||
| + | \\ | ||
| + | 2x + 4y = 6 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | es equivalente a este otro | ||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}{l} | ||
| + | 2x = -1 + 3y | ||
| + | \\ | ||
| + | 2x = 6 -4y | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | El segundo sistema lo he obtenido pasando los terminos en | ||
| + | <math> | ||
| + | y | ||
| + | </math> | ||
| + | del miembro de la izquierda al miembro de la derecha en cada una de las | ||
| + | ecuaciones del primer sistema. | ||
<br/> | <br/> | ||
| - | + | Del segundo sistema se deduce que | |
| + | <center> | ||
| + | <math> | ||
| + | -1 + 3y = 6 - 4y | ||
| + | </math> | ||
| + | </center> | ||
| + | que es una ecuación con una sola incognita cuya solución es | ||
| + | <math> | ||
| + | y = 1 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | Sustituyendo | |
| - | + | <math> | |
| - | + | y | |
</math> | </math> | ||
| - | | + | por 1 en la primera ecuación del sistema de partida se tiene que |
| + | <center> | ||
| + | <math> | ||
| + | 2x - 3 = -1 | ||
| + | </math> | ||
| + | </center> | ||
| + | que es una ecuación con una sola incognita y cuya solución es | ||
| + | <math> | ||
| + | x = 1 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ==Método de sustitución== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Supongamos que un sistema de ecuaciones se puede poner de la forma | ||
| + | <center> | ||
<math> | <math> | ||
| - | \left | + | \left\{ |
| - | + | \begin{array}{l} | |
| - | \ | + | a \cdot b + c = d |
| - | + | \\ | |
| + | a + e = f | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| + | </center> | ||
| + | Entonces podemos despejar | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | en la segunda ecuación y sustituirla en la primera, para obtener la ecuación: | ||
| + | <center> | ||
| + | <math> | ||
| + | \left( \, f - e \, \right) \cdot b + c = d | ||
| + | </math> | ||
| + | </center> | ||
| + | Lo que se busca es que esta ecuación dependa de menos incognitas que las de | ||
| + | partida. | ||
<br/> | <br/> | ||
| - | + | Aqui | |
<math> | <math> | ||
| - | \ | + | a, \, b, \, c, \, d, \, e |
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| + | y | ||
| + | <math> | ||
| + | f | ||
| + | </math> | ||
| + | son expresiones algebraicas de las incognitas del sistema. | ||
<br/> | <br/> | ||
| - | + | ===Ejemplo=== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Intentemos resolver | ||
| + | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| + | \begin{array}{l} | ||
| + | 4x + 3y = 7 | ||
| + | \\ | ||
| + | 2x - y = 1 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
| - | + | </center> | |
| + | La primera ecuación se puede reescribir de la forma | ||
| + | <center> | ||
| + | <math> | ||
| + | 2 \cdot \left( \, 2x \, \right) + 3y = 7 | ||
| + | </math> | ||
| + | </center> | ||
| + | Por otra parte, de la segunda ecuación del sistema se deduce que | ||
| + | <center> | ||
| + | <math> | ||
| + | 2x = 1 + y | ||
| + | </math> | ||
| + | </center> | ||
| + | Sustituyendo | ||
| + | <math> | ||
| + | 2x | ||
| + | </math> | ||
| + | por | ||
| + | <math> | ||
| + | 1 + y | ||
| + | </math> | ||
| + | en | ||
| + | <center> | ||
| + | <math> | ||
| + | 2 \cdot \left( \, 2x \, \right) + 3y = 7 | ||
| + | </math> | ||
| + | </center> | ||
| + | se tiene que | ||
| + | <center> | ||
| + | <math> | ||
| + | 2 \cdot \left( \, 1 + y \, \right)+ 3y = 7 | ||
| + | </math> | ||
| + | </center> | ||
| + | que es una ecuación con solo una incognita y cuya solución es | ||
| + | <math> | ||
| + | y = 1 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| + | Sustituyendo | ||
| + | <math> | ||
| + | y | ||
| + | </math> | ||
| + | por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos | ||
| + | una ecuación de una sola incognita | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | 4 + 3y = 7 | |
</math> | </math> | ||
</center> | </center> | ||
| + | cuya solución es | ||
| + | <math> | ||
| + | x = 1 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | == | + | ==Método de Gauss== |
<br/> | <br/> | ||
| - | + | [[Imagen:gauss.jpg|frame|Gauss es uno de los matematicos mas | |
| + | importantes de todos los tiempos. ¡Fue un GENIO!]] | ||
<br/> | <br/> | ||
| - | + | El método de Gauss consiste en transformar el sistema dado en otro equivalente. | |
| + | Para ello tomamos la [[Definición y tipos#Definición|matriz ampliada]] del | ||
| + | sistema y mediante las [[Matriz inversa#Operaciones elementales con las filas de una matriz|operaciones elementales]] | ||
| + | con sus filas la transformamos en una [[¿Qué es una matriz?#Matrices triangulares superiores|matriz triangular superior]] ( o | ||
| + | [[¿Qué es una matriz?#Matrices triangulares inferiores|inferior]] ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil | ||
| + | de resolver. | ||
<br/> | <br/> | ||
| - | + | Es esencialmente el [[Métodos de resolución de sistemas de ecuaciones lineales#método de reducción|método de reducción]]. En el método de Gauss se | |
| + | opera con ecuaciones, como se hace en el método de reducción, pero uno se ahorra | ||
| + | el escribir las incognitas porque al ir los coeficientes de una misma incognita | ||
| + | siempre en una misma columna, uno sabe en todo momento cual es la incognita a la | ||
| + | que multiplican. | ||
<br/> | <br/> | ||
| - | + | ===Ejemplo=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | La matriz ampliada del sistema de ecuaciones: | |
<br/> | <br/> | ||
| Línea 152: | Línea 438: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \left\{ |
| - | + | \begin{array}[c]{ccc} | |
| - | + | x \, + \, y \, + \, z & = & ~~3 | |
| - | + | \\ | |
| - | + | x \, + \, y \, - \, z & = & ~~1 | |
| - | + | \\ | |
| - | + | x \, - \, y \, - \, z & = & -1 | |
| - | \right | + | \end{array} |
| + | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 165: | Línea 452: | ||
<br/> | <br/> | ||
| - | + | es: | |
<br/> | <br/> | ||
| Línea 171: | Línea 458: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | |||
\left( | \left( | ||
| - | \begin{array}[c]{ | + | \left. |
| - | + | \begin{array}[c]{ccc} | |
| - | + | ~~1 & ~~1 & ~~1 | |
| - | + | \\ | |
| - | + | ~~1 & ~~1 & -1 | |
| - | \ | + | \\ |
| - | + | ~~1 & -1 & -1 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | \begin{array}[c]{c} | |
| - | + | ~~3 | |
| - | + | \\ | |
| - | + | ~~1 | |
| - | \right | + | \\ |
| - | + | -1 | |
| - | + | \end{array} | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
\right) | \right) | ||
</math> | </math> | ||
| Línea 200: | Línea 481: | ||
<br/> | <br/> | ||
| - | + | Si a la tercera y segunda fila le restamos la primera, obtenemos: | |
<br/> | <br/> | ||
| Línea 207: | Línea 488: | ||
<math> | <math> | ||
\left( | \left( | ||
| - | \begin{array}[c]{ | + | \left. |
| - | + | \begin{array}[c]{ccc} | |
| - | + | ~~1 & ~~1 & ~~1 | |
| - | + | \\ | |
| - | + | ~~0 & ~~0 & -2 | |
| + | \\ | ||
| + | ~~0 & -2 & -2 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \begin{array}[c]{c} | ||
| + | ~~3 | ||
| + | \\ | ||
| + | -2 | ||
| + | \\ | ||
| + | -4 | ||
| + | \end{array} | ||
\right) | \right) | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
</math> | </math> | ||
</center> | </center> | ||
| Línea 239: | Línea 510: | ||
<br/> | <br/> | ||
| - | + | Lo que acabamos de hacer es equivalente a restar a la tercera y segunda | |
| - | + | ecuación la primera. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Si ahora intercambiamos la segunda y tercera filas ( ecuaciones ), obtenemos | |
<br/> | <br/> | ||
| - | + | <center> | |
| - | < | + | |
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\left( | \left( | ||
| - | \ | + | \left. |
| - | \ | + | \begin{array}[c]{ccc} |
| - | + | ~~1 & ~~1 & ~~1 | |
| - | & | + | \\ |
| - | + | ~~0 & -2 & -2 | |
| - | + | \\ | |
| - | + | ~~0 & ~~0 & -2 | |
| + | \end{array} | ||
| + | \right| | ||
| + | \begin{array}[c]{c} | ||
| + | ~~3 | ||
| + | \\ | ||
| + | -4 | ||
| + | \\ | ||
| + | -2 | ||
| + | \end{array} | ||
\right) | \right) | ||
</math> | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | que es la matriz ampliada del sistema de ecuaciones: | |
<br/> | <br/> | ||
| - | + | <center> | |
| - | + | <math> | |
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | x \, + \, y \, + \, z & = & ~~3 | ||
| + | \\ | ||
| + | -2y \, - \, 2z & = & -4 | ||
| + | \\ | ||
| + | -2z & = & -2 | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | que es equivalente al inicial. | |
| + | |||
| + | <br/> | ||
| + | |||
| + | Solucionamos la tercera ocuacion para obtener | ||
<math> | <math> | ||
| - | + | z | |
</math> | </math> | ||
| - | | + | : |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 304: | Línea 578: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | z \, = \, 1 | |
</math> | </math> | ||
</center> | </center> | ||
<br/> | <br/> | ||
| - | + | En la primera y segunda ecuación, sustituimos | |
| - | + | ||
<math> | <math> | ||
| - | + | z | |
</math> | </math> | ||
| - | por | + | por la solucion de la tercera ecuación ( |
<math> | <math> | ||
| - | + | 1 \to z | |
</math> | </math> | ||
| - | | + | ), para obtener: |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 333: | Línea 597: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left\{ | |
| + | \begin{array}[c]{rcl} | ||
| + | x \, + \, y \, + \, 1 & = & ~~3 | ||
| + | \\ | ||
| + | -2y \, - \, 2 & = & -4 | ||
| + | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 339: | Línea 609: | ||
<br/> | <br/> | ||
| - | + | La segunda ecuación es ahora una ecuación con una sola incognita, | |
<math> | <math> | ||
| - | + | y | |
</math> | </math> | ||
| - | + | , que resolvemos para obtener | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | | + | |
<math> | <math> | ||
| - | + | y \, = \, 1 | |
</math> | </math> | ||
| + | . Sustituimos, en la primera ecuación, | ||
| + | <math> | ||
y | y | ||
| + | </math> | ||
| + | por 1 ( | ||
<math> | <math> | ||
| - | + | 1 \to y | |
| - | </math> | + | </math> |
| - | + | ). Esto nos da una ecuación en | |
<math> | <math> | ||
| - | + | x | |
</math> | </math> | ||
| - | | + | : |
<br/> | <br/> | ||
| Línea 365: | Línea 635: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | x \, + \, 1 \, + \, 1 \, = \, 3 | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 371: | Línea 641: | ||
<br/> | <br/> | ||
| - | + | que al resolverla termina de darnos la solución del sistema de ecuaciones inicial: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | === | + | <center> |
| + | <math> | ||
| + | x \, = \, y \, = \, z \, = \, 1 | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | ==Método de la matriz inversa== | |
| - | + | ||
| - | + | Un sistema de ecuaciones lineales se puede escribir en [[Definición y tipos#Definición|forma matricial]]: | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
<center> | <center> | ||
| - | + | <math> | |
| - | + | \mathbf{A} \cdot \mathbf{X} \, = \, \mathbf{B} | |
| - | + | </math> | |
| - | + | </center> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Si | |
<math> | <math> | ||
| - | + | \mathbf{A}^{-1} | |
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
| - | es | + | existe, es decir, si |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
| - | </math> | + | </math> |
| + | es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda | ||
| + | la igualdad anterior por la izquierda por | ||
| + | <math> | ||
| + | \mathbf{A}^{-1} | ||
| + | </math> | ||
| + | , para obtener: | ||
<br/> | <br/> | ||
| - | = | + | <center> |
| + | <math> | ||
| + | \mathbf{X} \, = \, \mathbf{A}^{-1} \cdot \mathbf{B} | ||
| + | </math> | ||
| + | </center> | ||
<br/> | <br/> | ||
| - | + | que es la solución del sistema de ecuaciones lineales de matriz de coeficientes | |
| - | | + | |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | | + | y matriz de terminos independientes |
<math> | <math> | ||
| - | \mathbf{ | + | \mathbf{B} |
</math> | </math> | ||
| - | + | . | |
| - | < | + | |
| - | + | <br/> | |
| - | </ | + | |
| - | + | ==Regla de Cramer== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Imagen:cramer2.gif|frame|Gabriel Cramer nacio Ginebra ( Suiza ) 1704 y murio en 1752. A | ||
| + | él le debemos la regla que lleva su nombre. ¡Gracias Gabriel por tu contribución a las Matemáticas!]] | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede | ||
| + | utilizar cuando la matriz | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | de coeficientes del sistema es cuadrada y de determinante no nulo. El que | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | sea cuadrada significa que el numero de incognitas y el numero de ecuaciones | |
| - | + | coincide. | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Cuando el sistema de ecuaciones | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 471: | Línea 733: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left. | |
| - | \left | + | \begin{array}{c} |
| - | \begin{array}{ | + | a_{11} \cdot x_1 + a_{12} \cdot x_2 + \ldots a_{1n} \cdot x_n = b_1 |
| - | + | ||
\\ | \\ | ||
| - | + | a_{21} \cdot x_1 + a_{22} \cdot x_2 + \ldots a_{2n} \cdot x_n = b_2 | |
\\ | \\ | ||
| - | + | \dotfill | |
| + | \\ | ||
| + | a_{m1} \cdot x_1 + a_{m2} \cdot x_2 + \ldots a_{mn} \cdot x_n = b_m | ||
\end{array} | \end{array} | ||
| - | \right | + | \right\} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 486: | Línea 749: | ||
<br/> | <br/> | ||
| - | + | satisface las condiciones arriba mencionadas, su solución viene dada por: | |
<br/> | <br/> | ||
| Línea 492: | Línea 755: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | x_1 \, = \, \frac |
| - | + | { | |
| - | \left| | + | \left| |
| - | + | \begin{array}[c]{cccc} | |
| - | + | b_1 & a_{12} & \ldots & a_{1n} | |
| - | + | \\ | |
| - | + | b_2 & a_{22} & \ldots & a_{2n} | |
| - | + | \\ | |
| - | \ | + | \vdots & \vdots & \ddots & \vdots |
| - | & | + | \\ |
| - | \ | + | b_m & a_{m2} & \ldots & a_{mn} |
| - | \ | + | \end{array} |
| - | + | \right| | |
| - | + | } | |
| - | + | {|\mathbf{A}|} | |
| - | + | , \qquad \qquad x_2 \, = \, \frac | |
| - | + | { | |
| - | \right| | + | \left| |
| - | + | \begin{array}[c]{cccc} | |
| - | \ | + | a_{11} & b_1 & \ldots & a_{1n} |
| - | \left| | + | \\ |
| - | + | a_{21} & b_2 & \ldots & a_{2n} | |
| - | + | \\ | |
| - | + | \vdots & \vdots & \ddots & \vdots | |
| - | + | \\ | |
| - | + | a_{m1} & b_m & \ldots & a_{mn} | |
| - | \right| | + | \end{array} |
| - | \ | + | \right| |
| + | } | ||
| + | {|\mathbf{A}|}, \qquad \qquad \ldots \ldots | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | \ldots \ldots, \qquad \qquad x_n \, = \, \frac |
| - | \ | + | { |
| - | \ | + | \left| |
| - | + | \begin{array}[c]{cccc} | |
| - | + | a_{11} & a_{12} & \ldots & b_1 | |
| - | + | \\ | |
| - | + | a_{21} & a_{22} & \ldots & b_2 | |
| - | + | \\ | |
| - | + | \vdots & \vdots & \ddots & \vdots | |
| - | + | \\ | |
| - | + | a_{m1} & a_{m2} & \ldots & b_m | |
| - | \left| | + | \end{array} |
| - | + | \right| | |
| - | + | } | |
| - | + | {|\mathbf{A}|} | |
| - | + | \qquad \qquad | |
| - | + | ||
| - | \ | + | |
| - | & | + | |
| - | \ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \ | + | |
| - | \ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \ | + | |
| - | + | ||
| - | \ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | \right| | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 589: | Línea 813: | ||
<br/> | <br/> | ||
| - | + | En general | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| Línea 599: | Línea 819: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | x_i \, = \, \frac{|\mathbf{A}_i|}{|\mathbf{A}|} |
| - | + | ||
| - | \ | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 611: | Línea 825: | ||
<br/> | <br/> | ||
| - | + | donde | |
| + | <math> | ||
| + | \mathbf{A}_i | ||
| + | </math> | ||
| + | es la matriz que se obtiene sustituyendo la i-esima columna de | ||
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | | + | por la [[Definición y tipos|matriz de los terminos independientes]], |
| + | <math> | ||
| + | B | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | Consideremos el sistema de ecuaciones: | ||
<br/> | <br/> | ||
| Línea 621: | Línea 850: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left\{ | |
| - | + | \begin{array}[c]{rcl} | |
| - | \begin{array}{ | + | x \, + \, y \, = \, 2 |
| - | + | \\ | |
| - | \\ | + | x \, - \, y \, = \, 0 |
| - | + | \end{array} | |
| - | \\ | + | \right. |
| - | + | ||
| - | \end{array} | + | |
| - | \right | + | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 636: | Línea 862: | ||
<br/> | <br/> | ||
| - | + | En este sistema de ecuaciones lineales, la matriz | |
<math> | <math> | ||
\mathbf{A} | \mathbf{A} | ||
</math> | </math> | ||
| - | + | de los coeficientes es una matriz cuadrada y | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | |\mathbf{A}| \, = \, | |
| - | + | \left| | |
| - | + | \begin{array}[c]{cc} | |
| + | 1 & ~~1 | ||
| + | \\ | ||
| + | 1 & -1 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \, = \, -2 \neq 0 | ||
</math> | </math> | ||
| - | + | . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo: | |
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<center> | <center> | ||
<math> | <math> | ||
| - | \ | + | x \, = \, \frac |
| - | + | { | |
| - | + | \left| | |
| - | \ | + | \begin{array}[c]{cc} |
| - | + | 2 & ~~1 | |
| - | + | \\ | |
| - | + | 0 & -1 | |
| - | + | \end{array} | |
| - | + | \right| | |
| - | + | } | |
| - | \begin{array}{ | + | {|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1 |
| - | + | \qquad \qquad y \, = \, \frac | |
| - | \\ | + | { |
| - | + | \left| | |
| - | + | \begin{array}[c]{cc} | |
| - | + | 1 & 2 | |
| - | \end{array} | + | \\ |
| - | \right | + | 1 & 0 |
| + | \end{array} | ||
| + | \right| | ||
| + | } | ||
| + | {|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1 | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | <br/> | |
| - | + | ||
| - | <br> | + | |
| - | + | ||
| - | + | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 09:15 9 oct 2010
Tabla de contenidos |
Introducción
Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones.
Los métodos de igualación, sustitución y reducción consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas facil, ¿no?).
A estas ecuaciones, con solo una incognita, se llega a traves de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas.
Así, es posible que en uno de estos pasos de eliminación de incognitas se utilize un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se utilize otro método ( el de igualación, por ejemplo ).
Cada vez que se encuentra la solución para una incognita, se sustituye esta incognita por su solución para obtener asi ecuaciones con menos incognitas.
Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar para resolver sistemas de ecuaciones compatibles determinados e indeterminados.
Estos mismos métodos tambien pueden utilizarse para comprobar si un sistema de ecuaciones es compatible o no. La utilizacion de cualquiera de ellos conduciria, en el caso de que el sistema fuese incompatible, a una igualdad que es falsa, por ejemplo:
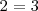
El método de la matriz inversa y la regla de Cramer solo se pueden utilizar en el caso de que el sistema de ecuaciones lineales sea compatible determinado.
Método de reducción
Consiste en multiplicar ecuaciones por numeros y sumarlas para reducir el número de incognitas hasta llegar a ecuaciones con solo una incognita.
Multiplicar una ecuación por un número consiste en multiplicar ambos miembros de la ecuación por dicho número.
Sumar dos ecuaciones consiste en obtener una nueva ecuación cuyo miembro derecho ( izquierdo ) es la suma de los miembros derechos ( izquierdos ) de las ecuaciones que se suman.
Ejemplo
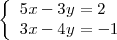
Multiplicando la primera ecuación por 3 y la segunda por -5, se obtienen las ecuaciones
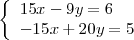
El sumar ambas ecuaciones nos da la ecuación
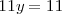
que es una ecuación con una sola incognita y cuya solución es
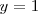
La elección de los factores 3 y -5 se ha hecho precisamente para que la
 desaparezca al sumar ambas ecuaciones.
desaparezca al sumar ambas ecuaciones.
Sutituyendo 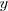 por uno en la primera ecuación del sistema de
ecuaciones de partida, se obtiene
por uno en la primera ecuación del sistema de
ecuaciones de partida, se obtiene
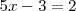
que es otra ecuación con una sola incognita y cuya solución es
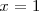 .
.
Método de igualación
El método de igualación consiste en lo siguiente:
Supongamos que tenemos dos ecuaciones:
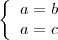
donde
 ,
,
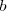 ,
y
,
y
 representan simplemente los miembros de estas ecuaciones ( son expresiones
algebraicas ).
representan simplemente los miembros de estas ecuaciones ( son expresiones
algebraicas ).
De las dos igualdades anteriores se deduce que
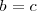
Si resulta que una incognita del sistema de ecuaciones no aparece ni en
 ni en
ni en
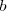 ,
entonces la ecuación
,
entonces la ecuación
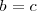
no contendría dicha incognita.
Este proceso de eliminación de incognitas se puede repetir varias veces hasta
llegar a una ecuación con solo una incognita, digamos
 .
.
Una vez que se obtiene la solución de esta ecuación se sustituye
 por su solución en otras ecuaciones dode aparezca
por su solución en otras ecuaciones dode aparezca
 para reducir el número de incognitas en dichas ecuaciones.
para reducir el número de incognitas en dichas ecuaciones.
Ejemplo
El sistema de ecuaciones
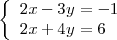
es equivalente a este otro
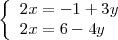
El segundo sistema lo he obtenido pasando los terminos en
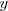 del miembro de la izquierda al miembro de la derecha en cada una de las
ecuaciones del primer sistema.
del miembro de la izquierda al miembro de la derecha en cada una de las
ecuaciones del primer sistema.
Del segundo sistema se deduce que
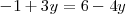
que es una ecuación con una sola incognita cuya solución es
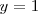 .
.
Sustituyendo
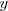 por 1 en la primera ecuación del sistema de partida se tiene que
por 1 en la primera ecuación del sistema de partida se tiene que
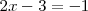
que es una ecuación con una sola incognita y cuya solución es
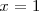 .
.
Método de sustitución
Supongamos que un sistema de ecuaciones se puede poner de la forma
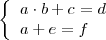
Entonces podemos despejar
 en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
en la segunda ecuación y sustituirla en la primera, para obtener la ecuación:
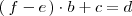
Lo que se busca es que esta ecuación dependa de menos incognitas que las de partida.
Aqui
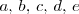 y
y
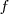 son expresiones algebraicas de las incognitas del sistema.
son expresiones algebraicas de las incognitas del sistema.
Ejemplo
Intentemos resolver
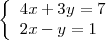
La primera ecuación se puede reescribir de la forma
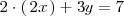
Por otra parte, de la segunda ecuación del sistema se deduce que
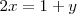
Sustituyendo
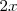 por
por
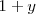 en
en
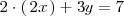
se tiene que
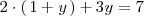
que es una ecuación con solo una incognita y cuya solución es
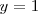 .
.
Sustituyendo
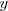 por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos
una ecuación de una sola incognita
por uno en la primera ecuación del sistema de ecuaciones de partida obtenemos
una ecuación de una sola incognita
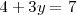
cuya solución es
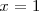 .
.
Método de Gauss
El método de Gauss consiste en transformar el sistema dado en otro equivalente. Para ello tomamos la matriz ampliada del sistema y mediante las operaciones elementales con sus filas la transformamos en una matriz triangular superior ( o inferior ). De esta forma obtenemos un sistema equivalente al inicial y que es muy facil de resolver.
Es esencialmente el método de reducción. En el método de Gauss se opera con ecuaciones, como se hace en el método de reducción, pero uno se ahorra el escribir las incognitas porque al ir los coeficientes de una misma incognita siempre en una misma columna, uno sabe en todo momento cual es la incognita a la que multiplican.
Ejemplo
La matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{ccc}
x \, + \, y \, + \, z & = & ~~3
\\
x \, + \, y \, - \, z & = & ~~1
\\
x \, - \, y \, - \, z & = & -1
\end{array}
</pre>
<p>\right.](/images/math/math-b4daf9b08947470816a091c908c8b878.png)
es:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~1 & ~~1 & -1
\\
~~1 & -1 & -1
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
~~1
\\
-1
\end{array}
</pre>
<p>\right)](/images/math/math-9d6156e83361678f19df40db3ecf5638.png)
Si a la tercera y segunda fila le restamos la primera, obtenemos:
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & ~~0 & -2
\\
~~0 & -2 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-2
\\
-4
\end{array}
</pre>
<p>\right)](/images/math/math-45eb9fde313d2a75f1b05cd42aac6c52.png)
Lo que acabamos de hacer es equivalente a restar a la tercera y segunda ecuación la primera.
Si ahora intercambiamos la segunda y tercera filas ( ecuaciones ), obtenemos
![\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
~~1 & ~~1 & ~~1
\\
~~0 & -2 & -2
\\
~~0 & ~~0 & -2
\end{array}
\right|
\begin{array}[c]{c}
~~3
\\
-4
\\
-2
\end{array}
</pre>
<p>\right)](/images/math/math-0730ab56aabea929252d49dbf9595acc.png)
que es la matriz ampliada del sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, z & = & ~~3
\\
-2y \, - \, 2z & = & -4
\\
-2z & = & -2
\end{array}
</pre>
<p>\right.](/images/math/math-eb6ec9bc0f3d4f3655e297c2d80271fe.png)
que es equivalente al inicial.
Solucionamos la tercera ocuacion para obtener
 :
:
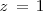
En la primera y segunda ecuación, sustituimos
 por la solucion de la tercera ecuación (
por la solucion de la tercera ecuación (
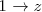 ), para obtener:
), para obtener:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, + \, 1 & = & ~~3
\\
-2y \, - \, 2 & = & -4
\end{array}
</pre>
<p>\right.](/images/math/math-5c98a4989cffb856e694abe6316e1767.png)
La segunda ecuación es ahora una ecuación con una sola incognita,
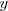 , que resolvemos para obtener
, que resolvemos para obtener
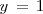 . Sustituimos, en la primera ecuación,
. Sustituimos, en la primera ecuación,
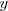 por 1 (
por 1 (
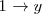 ). Esto nos da una ecuación en
). Esto nos da una ecuación en
 :
:

que al resolverla termina de darnos la solución del sistema de ecuaciones inicial:
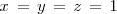
Método de la matriz inversa
Un sistema de ecuaciones lineales se puede escribir en forma matricial:

Si
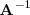 existe, es decir, si
existe, es decir, si
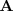 es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
la igualdad anterior por la izquierda por
es una matriz cuadrada de determinante no nulo, entonces podemos multiplicar toda
la igualdad anterior por la izquierda por
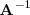 , para obtener:
, para obtener:
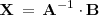
que es la solución del sistema de ecuaciones lineales de matriz de coeficientes
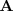 y matriz de terminos independientes
y matriz de terminos independientes
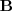 .
.
Regla de Cramer
Esta regla es un método de resolución de sistemas de ecuaciones lineales que se puede
utilizar cuando la matriz
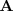 de coeficientes del sistema es cuadrada y de determinante no nulo. El que
de coeficientes del sistema es cuadrada y de determinante no nulo. El que
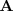 sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
coincide.
sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
coincide.
Cuando el sistema de ecuaciones
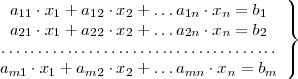
satisface las condiciones arriba mencionadas, su solución viene dada por:
![x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}, \qquad \qquad \ldots \ldots
x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}, \qquad \qquad \ldots \ldots](/images/math/math-57a8519773e4de96d9c3194f45f1c4b4.png)
![\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
\qquad \qquad
\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}
\qquad \qquad](/images/math/math-569b5d8f60f1d2e21c769b195d3609c9.png)
En general
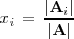
donde
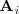 es la matriz que se obtiene sustituyendo la i-esima columna de
es la matriz que se obtiene sustituyendo la i-esima columna de
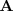 por la matriz de los terminos independientes,
por la matriz de los terminos independientes,
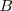 .
.
Ejemplo
Consideremos el sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-9d7fa2a713677bcaf5cea62fe4a5126f.png)
En este sistema de ecuaciones lineales, la matriz
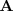 de los coeficientes es una matriz cuadrada y
de los coeficientes es una matriz cuadrada y
![|\mathbf{A}| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>
|\mathbf{A}| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>](/images/math/math-657d3399a3d5de5fef04047646d22644.png) . Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
. Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
![x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1
x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|\mathbf{A}|}\, = \, \frac{-2}{-2} \, = \, 1](/images/math/math-cc4c55b2e2b84ec9b768772cbfd55422.png)





