Cálculo del rango de una matriz
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | A una matriz cuadrada le podemos asociar un número que, como veremos con posterioridad, | ||
| + | nos permitirá estudiar y resolver un sistema de ecuaciones lineales y examinar si una | ||
| + | matriz dada posee matriz inversa y calcularla. | ||
| + | |||
| + | Este número que vamos a asociar a una matriz cuadrada lo llamaremos determinante de dicha | ||
| + | matriz. Veamos su calculo para matrices cuadradas de orden 2, y con posterioridad | ||
| + | calcularemos determinantes de matrices cuadradas de cualquier orden. | ||
| + | |||
| + | Para una matriz cuadrada de orden 2, | ||
| + | <math> | ||
| + | A = | ||
| + | \left( | ||
| + | \begin{array}[c]{cc} | ||
| + | a_{11} & a_{12} | ||
| + | \\ | ||
| + | a_{21} & a_{22} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | se llama determinante de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | al número real: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( A \right) = \left| A \right| = | ||
| + | \left| | ||
| + | \begin{array}{cc} | ||
| + | a_{11} & a_{12} | ||
| + | \\ | ||
| + | a_{21} & a_{22} | ||
| + | \end{array} | ||
| + | \right| | ||
| + | = a_{11} \cdot a_{22} - a_{12} \cdot a_{21} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | |||
| + | %% }}} | ||
| + | %% {{{ =Propiedades de los determinantes | ||
| + | En lo que sigue consideraremos | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | como una matriz cuadrada de orden | ||
| + | <math> | ||
| + | n; | ||
| + | </math> | ||
| + | | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | C_j | ||
| + | </math> | ||
| + | una fila y una columna cualesquiera de esa matriz. | ||
| + | El determinante de una matriz lo podemos ver como una función de sus filas | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( A \right) = \left| A \right| = | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_n \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | o de sus columnas | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( A \right) = \left| A \right| = | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_n \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Las propiedades mas importantes de los determinantes son: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 1. El determinante de una matriz cuadrada es igual al determinante de su matriz | ||
| + | traspuesta. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( A \right) = \makebox{det} \left( A^t \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 2. Si los elementos de una línea o columna de una matriz se multiplican por un número, el | ||
| + | determinante de la matriz queda multiplicado por dicho numero: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, t \cdot C_j, \, \ldots, \, C_n \right) | ||
| + | = t \cdot | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_j, \, \ldots, \, C_n \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, t \cdot F_i, \, \ldots, \, F_n \right) | ||
| + | = t \cdot | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_n \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 3. Si todas las lineas de una matriz de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | están multiplicadas por un mismo número | ||
| + | <math> | ||
| + | t | ||
| + | </math> | ||
| + | el determinante de la matriz queda multiplicado por | ||
| + | <math> | ||
| + | t^n: | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| t \cdot A \right| = t^n \cdot \left| A \right| | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 4. | ||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_j + C_j^\prime, \, \ldots, \, C_n \, | ||
| + | \right) | ||
| + | \, = \, | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_j, \, \ldots, \, C_n \, \right) | ||
| + | \, + \, | ||
| + | \makebox{det} \left( \, C_1, \, C_2, \, \ldots, \, C_j^\prime, \, \ldots, \, C_n \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i + F_i^\prime, \, \ldots, \, F_n \, | ||
| + | \right) | ||
| + | \, = \, | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \, = \, \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_n \, \right) | ||
| + | \, + \, | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i^\prime, \, \ldots, \, F_n \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 5. El determinante del producto de dos matrices cuadradas es igual al producto de los | ||
| + | determinantes de ambas matrices: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( A \cdot B \right) = \makebox{det} \left( A \right) \cdot \makebox{det} | ||
| + | \left( B \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 6. Si en una matriz cuadrada se permutan dos lineas, su determinante cambia de signo: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_i, \, \ldots, \, F_j, \, \ldots, \, | ||
| + | F_n \, \right) | ||
| + | = -\makebox{det} \left( \, F_1, \, F_2, \, \ldots, \, F_j, \, \ldots, \, F_i, \, \ldots, | ||
| + | \, F_n \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 7. Si una línea de una matriz cuadrada es combinacion lineal de las lineas restantes, es | ||
| + | decir, es el resultado de sumar los elementos de otras lineas multiplicadas por números | ||
| + | reales, su determinante es cero. Consecuencia inmediata de esta propiedad es que si una | ||
| + | matriz tiene una línea de ceros su determinante es cero. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 8. Si a los elementos de una línea de una matriz cuadrada se les suma una combinacion | ||
| + | lineal de las líneas restantes, su determinante no varia. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El metodo de Chío consiste en hacer cero el mayor número posible de elementos de una | ||
| + | línea utilizando las propiedad anterior de los determinantes y posteriormente desarrollar | ||
| + | el determinante por los adjuntos de los elementos de esa linea en la que hemos hecho | ||
| + | ceros. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | %% }}} | ||
| + | %% {{{ =Desarrollo de un determinante | ||
| + | |||
| + | En esta sección se explica un procedimiento que nos permite calcular determinantes de | ||
| + | cualquier orden, pero antes hemos de introducir los conceptos de '''''menor complementario''''', '''''adjunto''''' y '''''matriz adjunta'''''. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Menor complementario== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para una matriz cuadrada de orden | ||
| + | <math> | ||
| + | n, \, A = \left( \, a_{ij} \, \right), | ||
| + | </math> | ||
| + | se llama '''''menor complementario''''' del elemento | ||
| + | <math> | ||
| + | a_{ij}, | ||
| + | </math> | ||
| + | y lo representamos por | ||
| + | <math> | ||
| + | \alpha_{ij}, | ||
| + | </math> | ||
| + | al determinante de la matriz cuadrada de orden | ||
| + | <math> | ||
| + | n - 1 | ||
| + | </math> | ||
| + | que resulta de suprimir la fila | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | y la columna | ||
| + | <math> | ||
| + | j | ||
| + | </math> | ||
| + | | ||
| + | de la matriz | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Los menores complementarios de la matriz | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A = | ||
| + | \left( | ||
| + | \begin{array}{ccc} | ||
| + | 1 & 2 & 3 | ||
| + | \\ | ||
| + | 4 & 5 & 6 | ||
| + | \\ | ||
| + | 7 & 8 & 9 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | son | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{ccc} | ||
| + | \alpha_{11} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 5 & 6 | ||
| + | \\ | ||
| + | 8 & 9 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{12} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 4 & 6 | ||
| + | \\ | ||
| + | 7 & 9 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{13} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 4 & 5 | ||
| + | \\ | ||
| + | 7 & 8 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \\ | ||
| + | & & | ||
| + | \\ | ||
| + | \alpha_{21} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 2 & 3 | ||
| + | \\ | ||
| + | 8 & 9 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{22} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 3 | ||
| + | \\ | ||
| + | 7 & 9 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{23} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 7 & 8 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}[c]{ccc} | ||
| + | \alpha_{31} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 2 & 3 | ||
| + | \\ | ||
| + | 5 & 6 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{32} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 3 | ||
| + | \\ | ||
| + | 4 & 6 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | & | ||
| + | \qquad \alpha_{33} = | ||
| + | \left| | ||
| + | \begin{array}[c]{cc} | ||
| + | 1 & 2 | ||
| + | \\ | ||
| + | 4 & 5 | ||
| + | \end{array} | ||
| + | \right| | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Matriz adjunta== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para una matriz cuadrada de orden | ||
| + | <math> | ||
| + | n, \, A = \left( \, a_{ij} \, \right), | ||
| + | </math> | ||
| + | se llama '''''adjunto''''' del elemento | ||
| + | <math> | ||
| + | a_{ij}, | ||
| + | </math> | ||
| + | y lo representamos por | ||
| + | <math> | ||
| + | A_{ij}, | ||
| + | </math> | ||
| + | al producto | ||
| + | <math> | ||
| + | \left( \, -1 \, \right)^{i + j} \cdot \alpha_{ij} | ||
| + | </math>, es decir: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A_{ij} = \left( \, -1 \, \right)^{i + j} \cdot \alpha_{ij} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La matriz cuyos elementos son los adjuntos de los elementos de una matriz cuadrada | ||
| + | | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | se llama '''''matriz adjunta''''' de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | y se denota por | ||
| + | <math> | ||
| + | \makebox{Adj} \left( A \right) | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Los adjuntos de la matriz | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | del ejemplo anterior son: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{ccccccccccc} | ||
| + | A_{11} & = & -3 & \qquad & A_{12} & = & ~~~6 & \qquad & A_{13} & = & -3 | ||
| + | \\ | ||
| + | A_{21} & = & ~~6 & \qquad & A_{22} & = & -12 & \qquad & A_{23} & = & ~~6 | ||
| + | \\ | ||
| + | A_{31} & = & -3 & \qquad & A_{32} & = & ~~~6 & \qquad & A_{33} & = & -3 | ||
| + | &\end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La matriz adjunta de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | es | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{Adj} \left( A \right) = | ||
| + | \left( | ||
| + | \begin{array}{ccc} | ||
| + | -3 & ~~~6 & -3 | ||
| + | \\ | ||
| + | ~~6 & -12 & ~~6 | ||
| + | \\ | ||
| + | -3 & ~~~6 & -3 | ||
| + | \end{array} | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Desarrollo de un determinante== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El determinante de una matriz cuadrada de orden <math> n </math> es igual a la suma de los productos de los elementos | ||
| + | de una línea o columna cualquiera por sus adjuntos respectivos. Simbolicamente: | ||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, A \, \right) \, = \, a_{i1} \cdot A_{i1} + a_{i2} \cdot A_{i2} + \ldots + a_{in} \cdot A_{in} | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | \makebox{det} \left( \, A \, \right) \, = \, a_{1j} \cdot A_{1j} + a_{2j} \cdot A_{2j} + \ldots + a_{nj} \cdot A_{nj} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | |||
| + | %% }}} | ||
| + | %% {{{ =Cálculo de la inversa de una matriz | ||
| + | La '''''matriz inversa''''' de una matriz cuadrada | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | , es la matriz, | ||
| + | <math> | ||
| + | A^{-1} | ||
| + | </math> | ||
| + | , de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | que verifica: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot A^{-1} = A^{-1} \cdot A = I | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices | ||
| + | singulares. | ||
| + | |||
| + | Antes de calcular la matriz inversa de una dada hemos de asegurarnos de que efectivamente | ||
| + | existe la matriz inversa. Para ello utilizamos la siguiente propiedad: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \, \, \makebox{es regular} \Leftrightarrow \left| A \right| \neq 0 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una vez que hemos asegurado la existencia de la matriz inversa, calculamos esta mediante | ||
| + | la siguiente expresion: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A^{-1} = \frac{1}{\left| A \right|} \cdot | ||
| + | \left[ | ||
| + | \makebox{Adj} | ||
| + | \left( | ||
| + | \, A \, | ||
| + | \right) | ||
| + | \right] | ||
| + | ^t | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | donde | ||
| + | <math> | ||
| + | \makebox{Adj} | ||
| + | \left( | ||
| + | \, A \, | ||
| + | \right) | ||
| + | </math> | ||
| + | es la [[Desarrollo de un determinante| matriz adjunta]] de | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | . Se verifica que | ||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| A^{-1} \right| = \frac{1}{\left| A \right|} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | %% }}} | ||
| + | %% {{{ =Calculo del rango de una matriz | ||
| + | |||
En este epígrafe vamos a ver otro procedimiento para calcular el rango de una matriz | En este epígrafe vamos a ver otro procedimiento para calcular el rango de una matriz | ||
mediante determinantes. | mediante determinantes. | ||
| - | Se llama '''menor de orden k''' de una matriz | + | Se llama '''''menor de orden k''''' de una matriz |
<math> | <math> | ||
A | A | ||
| Línea 13: | Línea 638: | ||
| | ||
| - | El rango de una matriz es el orden del mayor menor no nulo que podemos obtener de esta | + | El '''''rango de una matriz''''' es el orden del mayor menor no nulo que podemos obtener |
| - | matriz. | + | de esta matriz. |
Si el rango de una matriz es k, entonces todos los menores de orden superior a k son | Si el rango de una matriz es k, entonces todos los menores de orden superior a k son | ||
nulos. | nulos. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
| + | |||
| + | %% }}} | ||
Revisión de 13:08 12 ene 2007
A una matriz cuadrada le podemos asociar un número que, como veremos con posterioridad, nos permitirá estudiar y resolver un sistema de ecuaciones lineales y examinar si una matriz dada posee matriz inversa y calcularla.
Este número que vamos a asociar a una matriz cuadrada lo llamaremos determinante de dicha matriz. Veamos su calculo para matrices cuadradas de orden 2, y con posterioridad calcularemos determinantes de matrices cuadradas de cualquier orden.
Para una matriz cuadrada de orden 2,
![A =
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
</pre>
<p>\right)
A =
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
</pre>
<p>\right)](/images/math/math-6b5b034dbef9fbb4d9ad0eac822a6009.png) se llama determinante de
se llama determinante de
 al número real:
al número real:
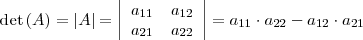
%% }}}
%% {{{ =Propiedades de los determinantes
En lo que sigue consideraremos
 como una matriz cuadrada de orden
como una matriz cuadrada de orden
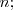
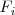 y
y
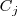 una fila y una columna cualesquiera de esa matriz.
El determinante de una matriz lo podemos ver como una función de sus filas
una fila y una columna cualesquiera de esa matriz.
El determinante de una matriz lo podemos ver como una función de sus filas
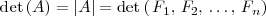
o de sus columnas
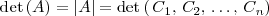
Las propiedades mas importantes de los determinantes son:
1. El determinante de una matriz cuadrada es igual al determinante de su matriz traspuesta.
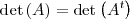
2. Si los elementos de una línea o columna de una matriz se multiplican por un número, el determinante de la matriz queda multiplicado por dicho numero:
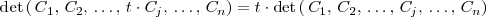
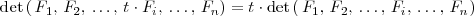
3. Si todas las lineas de una matriz de orden
 están multiplicadas por un mismo número
están multiplicadas por un mismo número
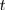 el determinante de la matriz queda multiplicado por
el determinante de la matriz queda multiplicado por
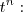
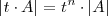
4.
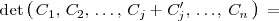
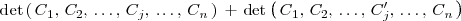
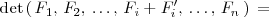
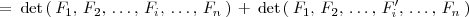
5. El determinante del producto de dos matrices cuadradas es igual al producto de los determinantes de ambas matrices:
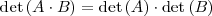
6. Si en una matriz cuadrada se permutan dos lineas, su determinante cambia de signo:
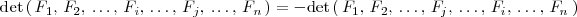
7. Si una línea de una matriz cuadrada es combinacion lineal de las lineas restantes, es decir, es el resultado de sumar los elementos de otras lineas multiplicadas por números reales, su determinante es cero. Consecuencia inmediata de esta propiedad es que si una matriz tiene una línea de ceros su determinante es cero.
8. Si a los elementos de una línea de una matriz cuadrada se les suma una combinacion lineal de las líneas restantes, su determinante no varia.
El metodo de Chío consiste en hacer cero el mayor número posible de elementos de una línea utilizando las propiedad anterior de los determinantes y posteriormente desarrollar el determinante por los adjuntos de los elementos de esa linea en la que hemos hecho ceros.
%% }}}
%% {{{ =Desarrollo de un determinante
En esta sección se explica un procedimiento que nos permite calcular determinantes de cualquier orden, pero antes hemos de introducir los conceptos de menor complementario, adjunto y matriz adjunta.
Tabla de contenidos |
Menor complementario
Para una matriz cuadrada de orden
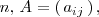 se llama menor complementario del elemento
se llama menor complementario del elemento
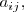 y lo representamos por
y lo representamos por
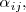 al determinante de la matriz cuadrada de orden
al determinante de la matriz cuadrada de orden
 que resulta de suprimir la fila
que resulta de suprimir la fila
 y la columna
y la columna
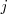 de la matriz
de la matriz

Ejemplo
Los menores complementarios de la matriz
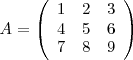
son
![\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-3783e29010f16c31576a73ebc6eb80c8.png)
![\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-03adb91ef28c3794b095ecb93b73fb77.png)
Matriz adjunta
Para una matriz cuadrada de orden
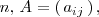 se llama adjunto del elemento
se llama adjunto del elemento
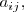 y lo representamos por
y lo representamos por
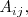 al producto
al producto
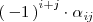 , es decir:
, es decir:
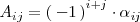
La matriz cuyos elementos son los adjuntos de los elementos de una matriz cuadrada
 se llama matriz adjunta de
se llama matriz adjunta de
 y se denota por
y se denota por
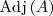
Ejemplo
Los adjuntos de la matriz
 del ejemplo anterior son:
del ejemplo anterior son:
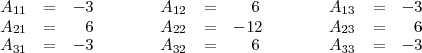
La matriz adjunta de
 es
es
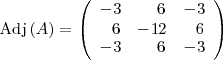
Desarrollo de un determinante
El determinante de una matriz cuadrada de ordenes igual a la suma de los productos de los elementos de una línea o columna cualquiera por sus adjuntos respectivos. Simbolicamente:
%% }}}
%% {{{ =Cálculo de la inversa de una matriz
La matriz inversa de una matriz cuadrada
 de orden
de orden
 , es la matriz,
, es la matriz,
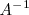 , de orden
, de orden
 que verifica:
que verifica:
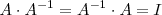
Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices singulares.
Antes de calcular la matriz inversa de una dada hemos de asegurarnos de que efectivamente existe la matriz inversa. Para ello utilizamos la siguiente propiedad:
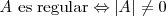
Una vez que hemos asegurado la existencia de la matriz inversa, calculamos esta mediante la siguiente expresion:
donde
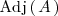 es la matriz adjunta de
es la matriz adjunta de
 . Se verifica que
. Se verifica que
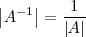
%% }}}
%% {{{ =Calculo del rango de una matriz
En este epígrafe vamos a ver otro procedimiento para calcular el rango de una matriz mediante determinantes.
Se llama menor de orden k de una matriz
 al determinante de orden k que está formado por los elementos que pertenecen a k
filas y a k columnas de la matriz
al determinante de orden k que está formado por los elementos que pertenecen a k
filas y a k columnas de la matriz

El rango de una matriz es el orden del mayor menor no nulo que podemos obtener de esta matriz.
Si el rango de una matriz es k, entonces todos los menores de orden superior a k son nulos.
%% }}}
Tweet

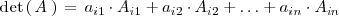
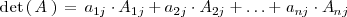
![A^{-1} = \frac{1}{\left| A \right|} \cdot
\left[
\makebox{Adj}
\left(
\, A \,
\right)
\right]
^t
A^{-1} = \frac{1}{\left| A \right|} \cdot
\left[
\makebox{Adj}
\left(
\, A \,
\right)
\right]
^t](/images/math/math-f567befc24c749b340e529b2c5d18d12.png)

