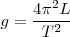El péndulo simple
De Wikillerato
Llamamos péndulo simple al formado por un hilo inextensible, de masa despreciable, suspendido por uno de sus extremos de un punto fijo y, que en el otro, lleva suspendida una masa. Al ser desplazado de la posición de equilibrio ángulos muy pequeños, el rozamiento del hilo con el punto de sujeción es despreciable.
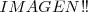
En la figura de la derecha observamos el sistema en equilibrio, el hilo vertical, de longitud 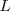 , sosteniendo la masa
, sosteniendo la masa 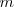 , de modo que la tensión del hilo es igual al peso.
, de modo que la tensión del hilo es igual al peso.
Tenemos pues que 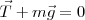 , o lo que es igual
, o lo que es igual 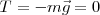
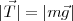
En la figura de la izquierda, hemos desplazado la masa 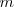 de modo que el hilo ha descrito un pequeño ángulo
de modo que el hilo ha descrito un pequeño ángulo 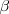 con relación a la vertical. Al dejar el sistema en libertad comienza a oscilar alrededor de la posición de equilibrio, manteniéndose sobre un plano.
con relación a la vertical. Al dejar el sistema en libertad comienza a oscilar alrededor de la posición de equilibrio, manteniéndose sobre un plano.
La masa 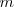 se ha elevado
se ha elevado 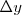 con relación a la horizontal, ha adquirido pues una energía potencial
con relación a la horizontal, ha adquirido pues una energía potencial 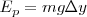 .
.
Al soltar 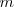 , describe un arco de circunferencia, de modo que, al caer al punto más bajo de la trayectoria, ha adquirido una energía cinética
, describe un arco de circunferencia, de modo que, al caer al punto más bajo de la trayectoria, ha adquirido una energía cinética 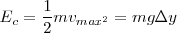
Debido a la propia energía cinética m vuelve a alcanzar la altura inicial. El péndulo oscila pues alrededor de la posición de equilibrio.
Hagamos un estudio de las fuerzas aplicadas. En el equilibrio sólo existen la tensión y el peso de m, pero en cualquier otra posición, la suma de la tensión 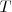 y el peso
y el peso 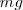 debe ser igual a la fuerza responsable del movimiento, tangente al arco de circunferencia descrito.
debe ser igual a la fuerza responsable del movimiento, tangente al arco de circunferencia descrito.
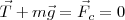
Observamos que el vector 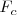 es un vector que recupera la posición de equilibrio.
es un vector que recupera la posición de equilibrio.
Pero si estudiamos en la figura el triángulo rectángulo que forman los tres vectores, observamos que
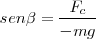
Pero para ángulos muy pequeños 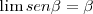
Con lo cual nos queda 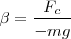
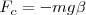
Por otra parte, sabemos que para ángulos muy pequeños, ángulo x radio = longitud del arco
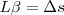
y la longitud del arco es aproximadamente igual a la longitud de la cuerda.
Nos queda 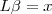 , siendo
, siendo  la proyección del arco sobre la cuerda, sustituyendo en
la proyección del arco sobre la cuerda, sustituyendo en 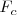
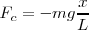
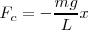
Dado que 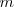 ,
, 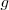 y
y 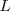 , son constantes, observamos que
, son constantes, observamos que 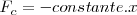
Es una fuerza igual a una constante por la separación de la posición de equilibrio y con signo opuesto, que responde a las condiciones del movimiento oscilatorio armónico
Aplicando la ecuación fundamental de la dinámica
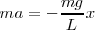
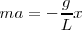
Sabemos que 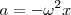 , tendremos que
, tendremos que 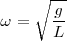
Pero 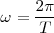
Con lo cual queda, 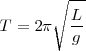
Como puede observarse, el periodo sólo depende de la longitud 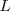 del pédulo y del valor de la gravedad en el punto.
del pédulo y del valor de la gravedad en el punto.
Esto nos permite calcular experimentalmente el valor de 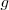 en un lugar cualquiera:
en un lugar cualquiera: