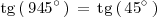Reducción de las razones trigonometricas
De Wikillerato
En este apartado veremos que las razones trigonométricas de cualquier angulo son
calculables a partir de las de ángulos comprendidos entre
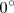 y
y 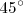 .
.
Para ello utilizaremos la siguiente tabla:
Por ejemplo, para conocer cual es la relación entre el coseno de
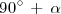 y las razones trigonometricas de
y las razones trigonometricas de
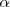 , mirariamos a la celda situada en la quinta columna y segunda fila, para encontrar que:
, mirariamos a la celda situada en la quinta columna y segunda fila, para encontrar que:
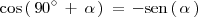
Las relaciones que muestran la tabla se pueden obtener a partir de la formulas del coseno y del seno de la suma y de la diferencia de dos angulos. Por ejemplo:
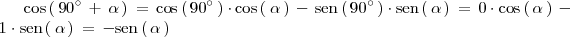
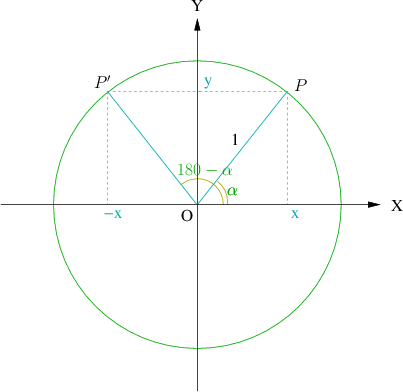
Otra manera de obtener las relaciones que muestran la tabla es representando ambos
angulos en la circunferencia goniometrica. Por ejemplo, si representamos en la
circunferencia goniometrica
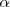 y
y
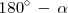 :
:
se observa facilmente que el coseno de
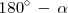 , la abcisa ( x ) del punto
, la abcisa ( x ) del punto
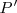 , coincide con el opuesto del coseno de
, coincide con el opuesto del coseno de
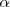 , la abcisa del punto
, la abcisa del punto
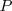 , y que el seno de
, y que el seno de
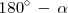 , la ordenada ( y ) del punto
, la ordenada ( y ) del punto
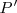 , coincide con el seno de
, coincide con el seno de
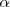 , la abcisa del punto
, la abcisa del punto
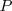 .
.
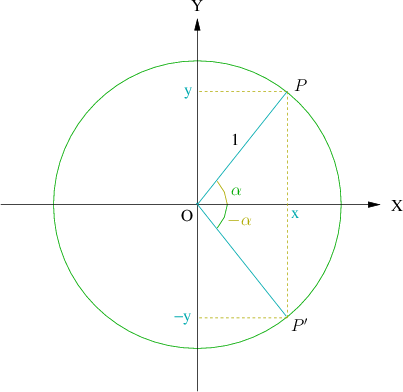
El mismo ejercicio se puede realizar con el resto de los angulos que se consideran en la
tabla. Invitamos al lector que compruebe por si mismo, mirando a la figura de abajo, que
las relaciones entre las razones trigonometricas de
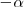 y
y
 que aparecen en la tabla son correctas.
que aparecen en la tabla son correctas.
Ejemplo
Veamos un ejemplo de como se puede utilizar la tabla de arriba para calcular la tangente de
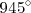 :
:
Si dividimos
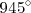 entre
entre
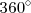 obtenemos como cociente
obtenemos como cociente
 y como resto
y como resto
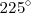 . Es decir:
. Es decir:
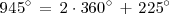
Utilizando la segunda columna de la tabla anterior, con
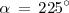 y
y
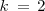 , tenemos que:
, tenemos que:
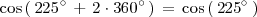
y
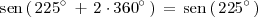
Así
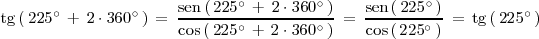
Por otra parte
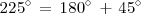
A partir de la cuarta fila de la tabla deducimos que:
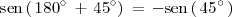
y
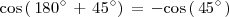
Por lo tanto,
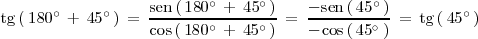
con lo cual