Definición y tipos
De Wikillerato
Tabla de contenidos |
Definición
Un sistema de ecuaciones lineales con incógnitas
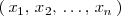 es un conjunto formado por
es un conjunto formado por
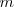 igualdades de la forma:
igualdades de la forma:
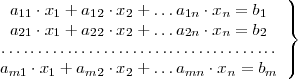
donde los
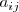 se llaman coeficientes y los
se llaman coeficientes y los
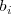 , terminos independientes del sistema.
, terminos independientes del sistema.
En los coeficientes
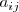 , el subindice
, el subindice
 indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice
indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice
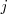 señala de que incognita es coeficiente
señala de que incognita es coeficiente
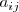 .
.
El subindice
 que aparece en el término
que aparece en el término
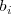 , indica la ecuación de la que
, indica la ecuación de la que
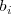 es término independiente.
es término independiente.
El sistema anterior de
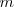 ecuaciones lineales con
ecuaciones lineales con
 incognitas se puede escribir matricialmente de la siguiente forma:
incognitas se puede escribir matricialmente de la siguiente forma:
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{c}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{array}
</pre>
<p>\right)
\, = \,
\left(
</p>
<pre> \begin{array}[c]{c}
b_1
\\
b_2
\\
\vdots
\\
b_m
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{c}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{array}
</pre>
<p>\right)
\, = \,
\left(
</p>
<pre> \begin{array}[c]{c}
b_1
\\
b_2
\\
\vdots
\\
b_m
\end{array}
</pre>
<p>\right)](/images/math/math-5e0cb3bd7b16ad7e059ce5fa38814c2a.png)
De izquierda a derecha, la primera matriz, en la igualdad anterior es la matriz de los coeficientes y la llamaremos
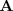 , la segunda matriz es la matriz de las incognitas y la llamaremos
, la segunda matriz es la matriz de las incognitas y la llamaremos
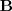 . La tercera es la matriz de los terminos indedependientes y la llamaremos
. La tercera es la matriz de los terminos indedependientes y la llamaremos
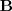 .
.
Con esta notación, nuestro sistema de ecuaciones lineales se puede representar de la siguiente manera:

La matriz de los coeficientes ampliada con los terminos independientes o
simplemente la
matriz ampliada es la matriz de los coeficientes,
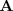 , a la que se añade la columna de los terminos independientes,
, a la que se añade la columna de los terminos independientes,
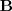 :
:
![\mathbf{A}|\mathbf{B} \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right|
\begin{array}[c]{c}
</p>
<pre> b_1
\\
b_2
\\
\vdots
\\
b_m
</pre>
<p>\end{array}
\right)
\mathbf{A}|\mathbf{B} \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right|
\begin{array}[c]{c}
</p>
<pre> b_1
\\
b_2
\\
\vdots
\\
b_m
</pre>
<p>\end{array}
\right)](/images/math/math-8cbf0649a3c06243987e57236ca3fdc1.png)
Solución de un sistema de ecuaciones lineales
Serán soluciones de un sistema de ecuaciones lineales todas las n-tuplas
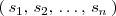 tales que al sustituir
tales que al sustituir
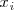 por
por
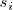 , para
, para
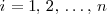 , todas las ecuaciones del sistema se conviertan en identidades.
, todas las ecuaciones del sistema se conviertan en identidades.
Al conjunto de todas las soluciones del sistema se le llama solución general, y a cada una de las soluciones que forman dicho conjunto, solución particular.
Ejemplo
La solución del sistema de ecuaciones lineales
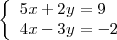
es
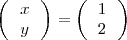
porque cuando sustituimos
 por 1 e
por 1 e
 por 2 en el sistema de ecuaciones, obtenemos
por 2 en el sistema de ecuaciones, obtenemos
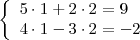
que son identidades ( igualdades ciertas ).
Tipos de sistemas de ecuaciones lineales
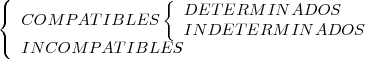
Sistemas de ecuaciones compatibles e incompatibles
Un sistema de ecuaciones lineales es compatible cuando tiene al menos una solución e incompatible cuando NO tiene ninguna solución.
Ejemplo
Un sistema de ecuaciones lineales incompatible es
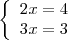
ya que de la primera ecuación se deduce que
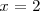 mientras que de la segunda se deduce que
mientras que de la segunda se deduce que
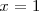
Como es imposible que
 sea dos y uno al mismo tiempo, ambas igualdades
sea dos y uno al mismo tiempo, ambas igualdades
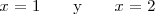
son incompatibles y por eso el sistema de ecuaciones con el que iniciabamos este ejemplo no tiene solución.
Teorema de Rouche-Fröbenius
Un sistema de
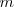 ecuaciones lineales con
ecuaciones lineales con
 incognitas es compatible ( tiene solución ) si, y sólo si, el rango de la matriz de los coeficientes coincide con el rango de la matriz
ampliada.
incognitas es compatible ( tiene solución ) si, y sólo si, el rango de la matriz de los coeficientes coincide con el rango de la matriz
ampliada.
Ejemplo:sistemas homogeneos
Un sistema de ecuaciones es homogéneo cuando todos sus terminos independientes son cero.
En un sistema de ecuaciones homogeneo, la matriz
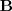 de los terminos independientes es una matriz nula, de manera que el
rango de la
matriz de los coeficientes y el de la
matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius,
que un sistema homogeneo SIEMPRE es compatible.
de los terminos independientes es una matriz nula, de manera que el
rango de la
matriz de los coeficientes y el de la
matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius,
que un sistema homogeneo SIEMPRE es compatible.
En cualquier sistema homogeneo, una solución particular es la solución trivial ( todas las incognitas son cero ).
Sistemas de ecuaciones lineales compatibles determinados
Un sistema de ecuaciones lineales es compatible determinado cuando tiene solución única.
Ejemplo
El sistema de ecuaciones lineales
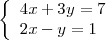
tiene una única solución
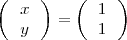
y se trata, por tanto, de un sistema de ecuaciones compatible determinado.
Sistemas de ecuaciones lineales compatibles indeterminados
Un sistema de ecuaciones lineales es compatible indeterminado cuando tiene infinitas soluciones.
Un sistema de ecuaciones lineales es compatible indeterminado si y solo si tiene mas de una solución, es decir:
Si un sistema de ecuaciones lineales tiene mas de una solución, entonces tiene infinitas soluciones.
Cuando el sistema de ecuaciones lineales es compatible indeterminado hay que distinguir entre la solución general del sistema de ecuaciones y las soluciones particulares del mismo.
Cuando se da la solución de un sistema de ecuaciones lineales compatible indeterminado lo que se da es un la solución general. Esta solución depende de uno o mas parametros.
Dando a los parametros unos valores determinados obtenemos una solución particular del sistema; dando a los parametros otros valores distintos obtenemos otra solución particular del sistema.
El número de parametros en la solución general coincide con el número de incognitas menos el rango de la matriz de los coeficientes del sistema.
Si el sistema es compatible, existen dos posibilidades:
1. Que el rango de la matriz de los coeficientes sea menor que el número de incognitas.
2. Que el rango de la matriz de los coeficientes sea igual al número de incognitas.
En el primer caso el sistema es compatible indeterminado y en el segundo caso el sistema es compatible determinado.
Ejemplo
El sistema de ecuaciones
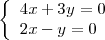
es homogeneo.
Como el determinante de la matriz de los coeficientes
![\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 3
\\
2 & -1
\end{array}
\right|
</pre>
<p>
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 3
\\
2 & -1
\end{array}
\right|
</pre>
<p>](/images/math/math-8bf1ca2b7a3a1a0a1c8e5fd3c58133a2.png)
es distinto de cero
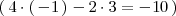 ,
el rango de
,
el rango de
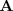 coincide con el número de incognitas ( 3 ) y, por lo tanto, el
sistema es compatible determinado, es decir tiene una solución única.
coincide con el número de incognitas ( 3 ) y, por lo tanto, el
sistema es compatible determinado, es decir tiene una solución única.
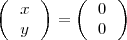
Ejemplo
El sistema de ecuaciones
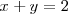
esta formado por una única ecuación y es compatible indeterminado, ya que tiene mas de dos soluciones.
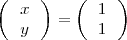
e
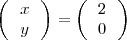
Para dar la solución de esta ecuación tenemos que introducir un parametro que
podemos llamar
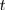 .
.
La solución general, en este caso, esta parametrizada por un solo parametro porque
número de incognitas ( 2 ) - rango de la matriz de los coeficientes( 1 ) = 1
La matriz de los coeficientes es una matriz con una fila y dos columnas
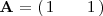
cuyo rango es 1 ( la unica manera posible de que una matriz tenga rango menor que 1 es teniendo todos sus elementos cero, en cuyo caso tendria rango cero ).
Si hacemos
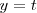 nos queda que
nos queda que

de manera que la solución general seria