Circunferencias tangentes de radio conocido

De Wikillerato

Procedimiento de resolución

El procedimiento principal para la resolución de problemas de tangencias es determinar si la distancia entre los centros es la suma o diferencia entre los radios.

Lugares geométricos

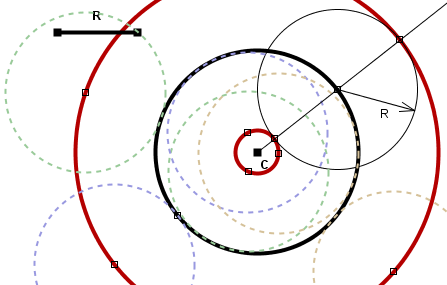
El lugar geométrico de los centros de todas las circunferencias de radio R conocido que pasan por un punto del plano fijo es la circunferencia con centro en el punto dado y radio R.

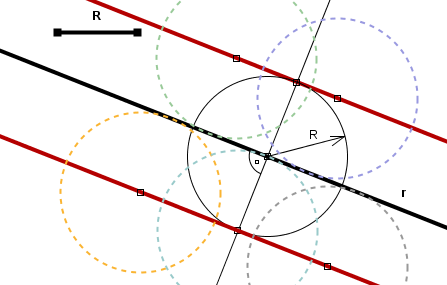
El lugar geométrico de los centros de todas las circunferencias de radio R conocido tangentes a una recta r dada son las dos rectas paralelas a r y situadas a una distancia R de la misma.

El lugar geométrico de los centros de todas las circunferencias de radio R conocido tangentes a una circunferencia de radio r dada son dos circunferencias concéntricas a la dada de radios R+r y |R-r|, respectivamente.

En efecto, si una circunferencia de radio R conocido ha de ser tangente a una recta o a una circunferencia dada, su centro deberá estar a una distancia de la recta o de la circunferencia igual a R. El lugar geométrico de los puntos que están a una distancia R de una recta dada son dos rectas paralelas a la recta dada, una a cada lado de la recta. Por su parte, el lugar geométrico de los puntos que están a una distancia R de una circunferencia dada son circunferencias concéntricas a la dada de radios R+r y |R-r|, siendo r el radio de la circunferencia dada. No importa cual de los radios R o r sea mayor; la expresión |R-r| siempre se interpretará como la diferencia entre el radio mayor y el radio menor.

En general, para dibujar una circunferencia de radio R conocido que sea tangente a dos elementos del plana o que pase por algún punto dado, habrá que determinar su centro como la intersección de dos de los lugares geométricos antes citados. En total, existen 6 casos diferentes, tal y como se detalla en los siguientes epígrafes.

Circunferencias de radio conocido que pasan por dos puntos dados

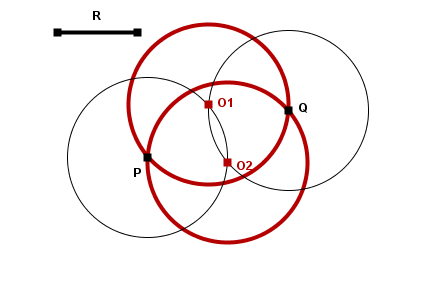
Para dibujar una las circunferencias de radio R conocido que pasan por dos puntos P y Q dados se trazarán sendos arcos de radio R con centro en los puntos P y Q. Los centros de las circunferencias solución estarán en la intersección de ambos arcos. Dichos arcos podrán ser tangentes, secantes o no cortarse, de manera que el problema podrá tener 1, 2 o ninguna solución, respectivamente.

Circunferencias de radio conocido tangentes a una recta y que pasan por un punto dado

Para hallar las circunferencias de radio R conocido que pasando por un punto P dado son tangentes a una recta r dada, se trazará una circunferencia de radio R con centro en P y la paralela a la recta r a una distancia R de la misma que esté situada en el mismo lado de la recta r que el punto P (de los dos semiplanos en que divide la recta r al plano, los centros de las circunferencias tangentes a r que pasan por P habrán de estar necesariamente en el semiplano que contiene a P, con lo cual no es necesario dibujar la paralela a r situada en el otro semiplano, ya que se sabe de antemano que no va a arrojar ninguna solución). Los puntos de intersección de la recta paralela con la circunferencia de centro P y radio R constituirán los centros de las circunferencias solución al problema. La paralela puede ser tangente, secante o no cortar a la circunferencia de centro P y radio R, existiendo entonces 1, 2 o ninguna circunferencia solución al problema, respectivamente.

Circunferencias de radio conocido tangentes a una circunferencia y que pasan por un punto dado

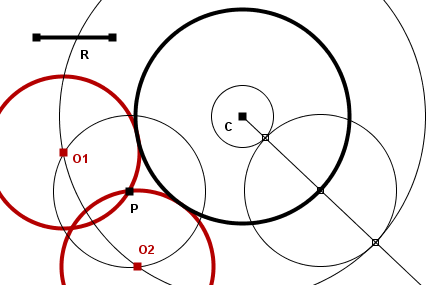
Para hallar las circunferencias de radio R conocido que pasando por un punto P dado son tangentes a una circunferencia dada de centro C y radio r, se trazará una circunferencia con centro en P y radio R y dos circunferencias con centro en C y radios R+r y |R-r|, respectivamente. Los puntos de intersección de dichas circunferencias serán los centros de las circunferencias que pasando por P y siendo tangentes a C tienen radio R. Los puntos de intersección situados sobre la circunferencia de radio R+r se corresponden con los centros de las circunferencias que son tangentes exteriores a C, mientras que los puntos de intersección situados sobre la circunferencia de radio |R-r| se corresponden con los centros de las circunferencias que son tangentes interiores a C.

La circunferencia de centro P y radio R podrá ser secante, tangente o no cortar a las circunferencias de radio R+r y de radio |R-r|, pudiendo existir 1, 2, 3, 4 o ninguna solución al problema (como mucho habrá dos circunferencias tangentes interiores a C y dos circunferencias tangentes exteriores a C que pasan por P y tienen radio R).

Circunferencias de radio conocido tangentes a dos rectas dadas

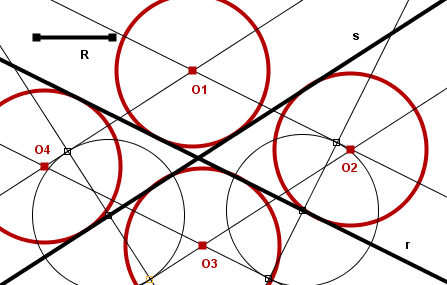
Para trazar las circunferencias de radio R conocido que son tangentes a dos rectas r y s dadas se trazarán las rectas paralelas a r y a s situadas a una distancia R de las mismas, a uno y otro lado. Las dos paralelas a r cortarán a las dos paralelas a s en cuatro puntos de intersección, que son los cuatro centros de las circunferencias solución al problema. Estos cuatro centros están situados en las bisectrices de los ángulos formados por las rectas r y s y son además los vértices de un rombo (un cuadrado si las rectas r y s son perpendiculares).

Si las rectas r y s fueran paralelas sólo será posible dibujar circunferencias de radio R tangentes a ambas cuando la distancia entre r y s sea igual a 2R, en cuyo caso existirán infinitas circunferencias tangentes a r y a s, siendo el lugar geométrico de sus centros la paralela a r y a s situada a mitad de distancia de ambas.

Texto en negrita== Circunferencias de radio conocido tangentes a dos circunferencias dadas ==

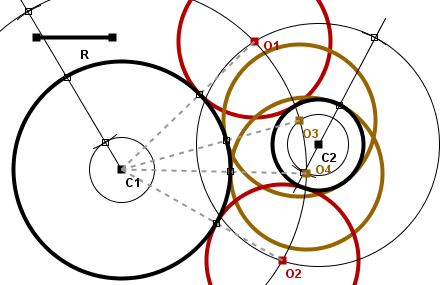
Para trazar las circunferencias de radio R conocido que son tangentes simultáneamente a una circunferencia de centro C1 y radio r1 y a otra circunferencia de centro C2 y radio r2, se trazarán dos circunferencias con centro en C1 y radios R+r1 y |R-r1|, respectivamente, y otras dos circunferencias con centro en C2 y radios R+r2 y |R-r2|, respectivamente. Los puntos de intersección de unas y otras circunferencias constituyen los centros de las circunferencias que solucionan el problema. Teniendo en cuenta que cada circunferencia puede cortar en 1, 2 o ningún punto a las otras dos circunferencias no concéntricas, el problema podrá tener entre 0 y 8 soluciones.

Los puntos de intersección situados sobre la circunferencia de radio R+r1 se corresponden con los centros de las circunferencias que son tangentes exteriores a C1, mientras que los puntos de intersección situados sobre la circunferencia de radio |R-r1| se corresponden con los centros de las circunferencias que son tangentes interiores a C1. De la misma forma, los puntos de intersección situados sobre la circunferencia de radio R+r2 se corresponden con los centros de las circunferencias que son tangentes exteriores a C2, mientras que los puntos de intersección situados sobre la circunferencia de radio |R-r2| se corresponden con los centros de las circunferencias que son tangentes interiores a C2. Esto tendrá que ser tenido en cuenta a la hora de dibujar las circunferencias concéntricas si únicamente quieren obtenerse circunferencias solución que sean tangentes interiores o exteriores a C1 y C2.

Circunferencias de radio conocido tangentes a una recta y a una circunferencia dadas

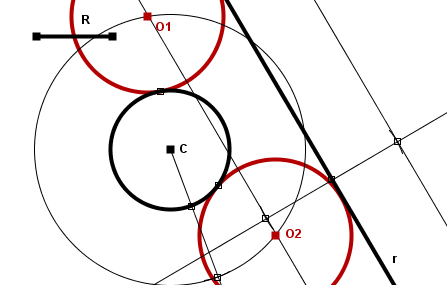
Para trazar la hijo puta de radio R conocido que son tangentes simultáneamente a una circunferencia dada de centro C y radio r y a una recta s dada, se trazarán las dos rectas paralelas a s que están a una distancia R de la misma (una situada a cada lado de s) y dos circunferencias con centro en C y radios R+r y |R-r|, respectivamente. Los puntos de intersección de las circunferencias concéntricas con las paralelas constituirán los centros de las circunferencias solución al problema. Cada paralela puede cortar a cada una de las circunferencias concéntricas a C en 1 (tangente), 2 (secante) o ningún punto, de manera que el problema puede tener entre 0 y 8 soluciones.

Si únicamente quieren obtenerse circunferencias tangentes exteriormente a C, sólo habrá que trazar la circunferencia de centro C y radio R+r. De la misma forma, si únicamente quieren obtenerse circunferencias tangentes interiormente a C, sólo habrá que trazar la circunferencia de centro C y radio |R-r|.

Enlaces externos

TRAZOIDE. Teoría y ejercicios resueltos de ENLACES y TANGENCIAS de CIRCUNFERENCIAS en Dibujo Técnico