Navegación
Ecuación de Schrödinger: ondas de probabilidad
De Wikillerato
(Diferencias entre revisiones)
| Línea 3: | Línea 3: | ||
<math>H</math> es el '''operador Hamiltoniano''': <math>H=-\frac{h}{2\pi i} \triangledown^2</math> | <math>H</math> es el '''operador Hamiltoniano''': <math>H=-\frac{h}{2\pi i} \triangledown^2</math> | ||
| - | <math>\triangledown^2</math> es el operador laplaciana e incluye derivadas parciales respecto a las coordenadas: <math>\triangledown^2=\frac{\partial^2}{\partial x^2}+\frac{\ | + | <math>\triangledown^2</math> es el operador laplaciana e incluye derivadas parciales respecto a las coordenadas: <math>\triangledown^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}</math>. |
<math>\Psi</math> es la '''función de onda''' del sistema: define al sistema en el espacio. La función de onda depende de las coordenadas del sistema y del spin. | <math>\Psi</math> es la '''función de onda''' del sistema: define al sistema en el espacio. La función de onda depende de las coordenadas del sistema y del spin. | ||
Revisión de 20:24 28 ene 2007
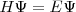
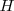es el operador Hamiltoniano: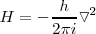 
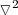es el operador laplaciana e incluye derivadas parciales respecto a las coordenadas: 
.
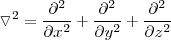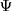es la función de onda del sistema: define al sistema en el espacio. La función de onda depende de las coordenadas del sistema y del spin.
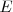es la energía del sistema: se trata de la energía total del sistema, por lo tanto incluye energía cinética y potencial
Aunque parezca una simple ecuación, es una de las ecuaciones más difíciles!. De hecho, sólo tiene soluciones exactas para el átomo de hidrógeno y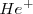 
.
