Introducción a las cónicas
De Wikillerato
| Línea 78: | Línea 78: | ||
<br/> | <br/> | ||
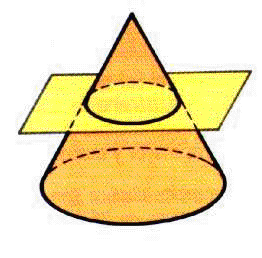
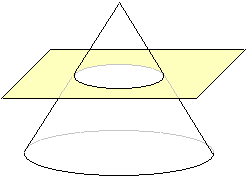
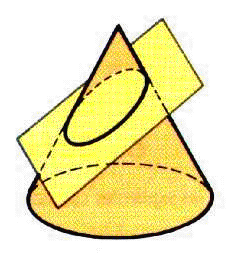
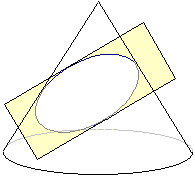
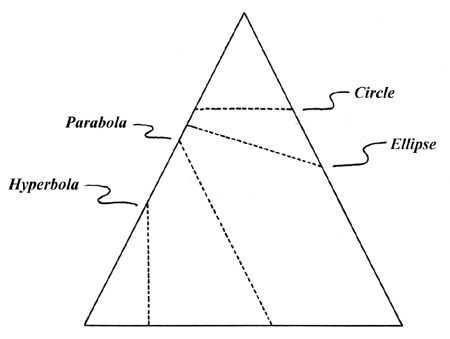
| - | [[Imagen:planosEnCono.png|frame| | + | [[Imagen:planosEnCono.png|frame|En esta figura de la izquierda teneis una superficie |
| - | + | cónica de revolución cortada por cuatro planos. En ella se indica el tipo de conica que | |
| - | + | forma la intersección de cada plano con la superficie cónica de revolución]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | : | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
Revisión de 17:24 12 ene 2007
Una superficie cónica de revolución es la superficie engendrada por una recta llamada generatriz, que gira alrededor de otra fija llamada eje, a la que corta en un punto denominado vértice.
Una conica es la curva que se obtiene como intersección de una superficie cónica de
revolución y un plano
 .
.
Dependiendo de la posición del plano
 con respecto a laperficie cónica, podemos obtener cinco cónicas distintas:
con respecto a laperficie cónica, podemos obtener cinco cónicas distintas:
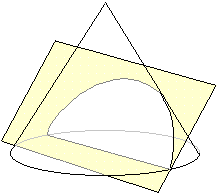
1. Si el plano es perpendicular al eje de la superficie cónica y no pasa por el vértice, la cónica es una circunferencia.
2. Si el plano es oblicuo al eje de la superficie cónica, corta a todas sus generatrices y no pasa por el vértice, la cónica es una curva cerrada que recibe el nombre de elipse.
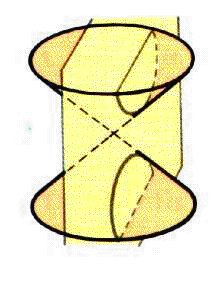
3. Si el plano es paralelo al eje de la superficie cónica, la cónica se denomina hipérbola, y es una curva que consta de dos partes, una en cada una de las hojas de la superficie cónica.
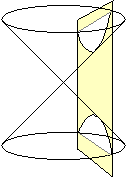
4. Si el plano es oblicuo al eje y paralelo a la generatriz, la cónica es una curva abierta denominada parábola.
5. Si el plano pasa por el vértice, decimos que la cónica es degenerada y puede ser un punto, una recta o un par de rectas concurrentes, dependiendo de si el plano secante tiene menos, igual o más inclinación que las generatrices.