Significado geométrico de la derivada
De Wikillerato
| Línea 127: | Línea 127: | ||
t | t | ||
</math> | </math> | ||
| - | es una [[ | + | es una [[La derivada como una tasa de variación instantánea|tasa de variación instantánea]], la [[Definición de derivada|derivada]] de |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
Revisión de 18:30 11 ene 2007
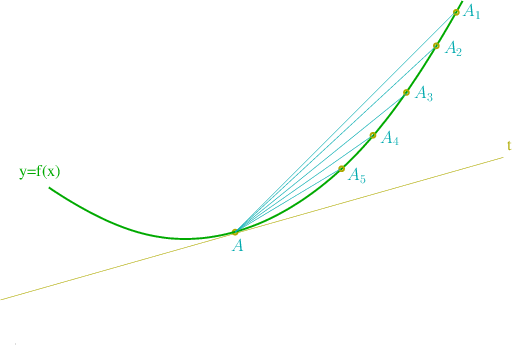
Consideremos la grafica de una función
 . Tomemos un punto
. Tomemos un punto
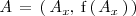 en dicha grafica y consideremos una sucesión de puntos
en dicha grafica y consideremos una sucesión de puntos
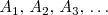 en la grafica de
en la grafica de
 . Supongamos que todos estos puntos estan a la derecha de
. Supongamos que todos estos puntos estan a la derecha de
 y que cuando
y que cuando
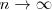 ,
,
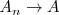 .
.
La recta que pasa por los puntos
 y
y
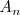 es una secante a la grafica de la función
es una secante a la grafica de la función
 . De esta forma, hay una secante para cada punto
. De esta forma, hay una secante para cada punto
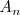 . Sea
. Sea
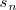 la recta que pasa por
la recta que pasa por
 y por
y por
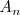 .
.
Cuando
 tiende a
tiende a
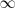 ,
,
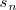 tiende a la tangente a la grafica de la función
tiende a la tangente a la grafica de la función
 en el punto
en el punto
 ,
,
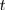 :
:
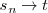
Habria de esperar, pues, que la pendiente de
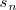 tienda a la pendiente de
tienda a la pendiente de
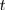 cuando
cuando
 tiende a
tiende a
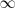 . La pendiente de
. La pendiente de
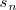 es una tasa de variación media, mientras que la
pendiente de
es una tasa de variación media, mientras que la
pendiente de
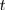 es una tasa de variación instantánea, la derivada de
es una tasa de variación instantánea, la derivada de
 en
en
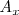 .
.