Patrocinado por PHPDocX

Síguenos en Twitter

Buscar en WikilleratO
   

Circunferencias tangentes conocido el punto de tangencia

De Wikillerato

(Diferencias entre revisiones)
(→Circunferencias tangentes a una recta o una circunferencia en un punto dado de la misma y tangentes además a una circunferencia dada)
(→Circunferencias tangentes a una recta o una circunferencia en un punto dado de la misma y tangentes además a una circunferencia dada)
Línea 41: Línea 41:
-
La solución a este problema se encuentra de forma sencilla aplicando conceptos de [[homotecia]], [[potencia]] o [[Inversión (Dibujo)| inversión]]. No obstante, también es posible encontrar una solución al problema (con un procedimiento algo más laborioso pero conceptualmente más elemental) sin recurrir a estos conceptos más avanzados. El procedimiento que se explica en este epígrafe es la resolución denominada habitualmente por "dilatación".
+
es una cosa redonda y su fórmula es P2+K2y a+a2=KK[Imagen:circunferencias_tangentes_recta_punto_tangencia_circunferencia_dilatacion.png|center|500px]]
-
 
+
-
Una dilatación de distancia R de una recta o de una circunferencia se define como el lugar geométrico de los puntos que están situados a una distancia R de dicha recta o circunferencia. Dada la definición anterior, estos lugares geométricos coincidirán con los lugares geométricos de los centros de una [[Circunferencias tangentes de radio conocido#Lugares geométricos|circunferencia de radio R tangente a la recta o circunferencia]] para la cual se quiere calcular su dilatación. Estos lugares geométricos serán dos rectas paralelas a la recta dilatada o dos [[Circunferencias concéntricas|circunferencias concéntricas]] con la circunferencia dada, respectivamente.
+
-
 
+
-
En particular, si se aplica una dilatación de valor R a una circunferencia de radio R, obtendremos una circunferencia de radio 2R y otra de radio cero, es decir, una dilatación de valor igual al radio de una circunferencia transforma dicha circunferencia en su centro. La dilatación es pues un mecanismo que permite transformar circunferencias en puntos.
+
-
 
+
-
Cuando dos o más elementos tangentes son dilatados con la misma distancia R, los elementos dilatados siguen siendo tangentes entre sí, es decir, la dilatación conserva las relaciones de tangencia. De esta forma, y teniendo en cuenta lo expuesto anteriormente, todo problema de tangencias en el que intervenga una circunferencia de radio R puede reducirse por dilatación a un problema de tangencias equivalente en el que sólo intervenga el centro de la circunferencia (por dilatación, transformamos una circunferencia en un punto).
+
-
 
+
-
Así pues, para hallar las circunferencias que son tangentes a una recta r en un punto T de la misma y a una circunferencia C de radio R, se obtendrán las dos rectas r' y r", paralelas a r, que resultan de dilatar r en la cantidad R. Como el centro de la circunferencia tangente a r en el punto T debe estar sobre la recta s, perpendicular a r en el punto T, entonces, al transformar el problema por dilatación, la circunferencia solución dilatada deberá ser tangente a r' en T' o a r" en T", siendo T' y T" los puntos de intersección de la recta s con las rectas r' y r", respectivamente.
+
-
 
+
-
El problema consiste ahora en trazar dos circunferencias: la circunferencia tangente a r' en el punto T' que pasa por C y la circunferencia tangente a r" en T" que pasa por C. Se sabe que los centros O1 y O2 de estas circunferencias estarán en la intersección de la recta s con las mediatrices de los segmenteos CT' y CT", respectivamente. Estos cenntros O1 y O2, además de ser centros de las circunferencias solución dilatadas, serán también centros de las circunferencias solución sin dilatar, ya que toda circunferencia y sus dilataciones son concéntricas.
+
-
 
+
-
Resumiendo, los pasos para trazar las circunferencias tangentes a una recta r dada en un punto T de la misma y que son a su vez tangentes a una circunferencia dada de centro C y radio R son los siguientes:
+
-
 
+
-
#Trácense las dos rectas r' y r" paralelas a r y situadas a una distancia R de la misma (dilatación de r de valor R).
+
-
#Trácese la recta s perpendicular a r en el punto T, que cortará a la recta r' en el punto T' y a la recta r" en el punto T".
+
-
#Hállese la mediatriz del segmento CT', que cortará a s en el punto O1.
+
-
#Hállese asimismo la mediatriz del segmento CT", que cortará a s en el punto O2.
+
-
#Las soluciones al problema serán las circunferencias con centros en O1 y O2 que pasan por el punto T.
+
-
 
+
-
 
+
-
[[Imagen:circunferencias_tangentes_recta_punto_tangencia_circunferencia_dilatacion.png|center|500px]]
+
[[Categoría:Dibujo]]
[[Categoría:Dibujo]]

Revisión de 21:21 12 nov 2008

Tabla de contenidos

Lugares geométricos

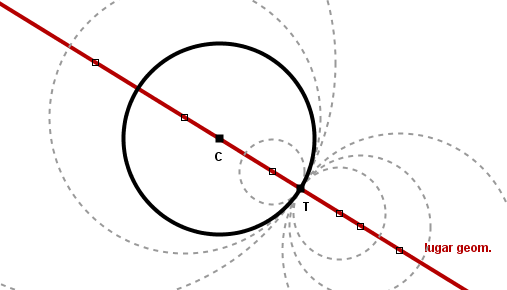
El lugar geométrico de los centros de todas las circunferencias tangentes a una recta r dada en un punto P de la misma es la recta perpendicular a r que pasa por el punto P.


Imagen:circunferencias_tangentes_recta_punto_tangencia.png


El lugar geométrico de los centros de todas las circunferencias tangentes a una circunferencia C dada en un punto P de la misma es la recta CP que une el centro de la circunferencia dada con el punto de tangencia. Los puntos de la recta CP situados en el exterior de la circunferencia C y a mayor distancia de C que de P corresponden a los centros de las circunferencias tangentes exteriores a C, mientras que los puntos de la recta CP situados en el interior de C o en su exterior pero a mayor distancia de P que de C corresponden a los centros de las circunferencias tangentes interiores a C.


Imagen:circunferencias_tangentes_circunferencia_punto_tangencia.png

Circunferencia tangente a una recta o una circunferencia en un punto dado de la misma y que pasa por otro punto dado

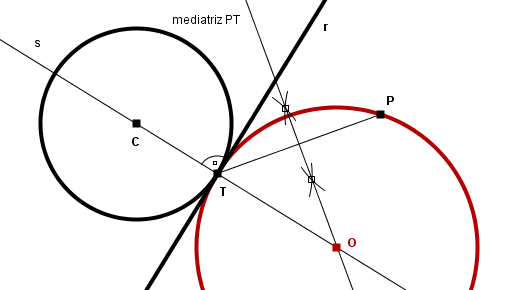
Sea una recta r o una circunferencia C y sea T un punto perteneciente a la misma. Sea s la recta lugar geométrico de los centros de todas las circunferencias tangentes a r o C en el punto T, conforme a lo especificado en el párrafo anterior.

Se desean trazar las circunferencias tangentes a r o C en el punto T y que pasan por otro punto P. El centro de la circunferencia solución debe estar sobre la recta s y además debe estar a la misma distancia de T que de P. Por lo tanto, el centro de la circunferencia solución estará en la intersección de la recta s con la mediatriz del segmento PT.


Imagen:circunferencia_tangente_recta_punto_tangencia_punto.png

Circunferencia tangente a una recta o una circunferencia en un punto dado de la misma y tangente además a una recta dada

Se conoce el punto T, que pertenece a una recta r o a una circunferencia C dada. Se quiere trazar la circunferencia que siendo tangente a r o C en el punto T es asimismo tangente a otra recta t dada. Nótese que si una circunferencia ha de ser tangente a otra circunferencia C en el punto T de la misma, también será tangente a la recta perpendicular a CT que pasa por el punto T. Si denotamos por r' a esta recta perpendicular, se tiene que los dos problemas planteados en este apartado son el mismo: trazar la circunferencia tangente a la recta r (o r' en el caso de que el dato sea una circunferencia) en el punto T de la misma, y que es además tangentes a otra recta t dada.

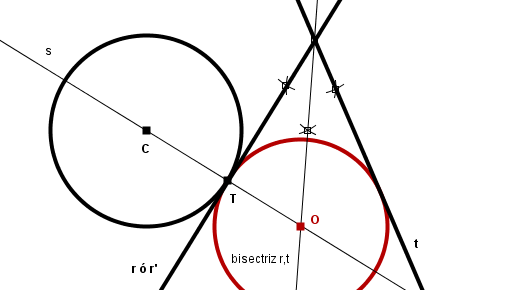
El centro de la circunferencia solución buscada tendrá que estar a la misma distancia de la recta r (o r') que de la recta t (por ser tangente a ambas), es decir, debe estar en la bisectriz del ángulo formado por las rectas r (o r') y t. Por otra parte, el centro de la circunferencia solución debe estar también sobre la recta s, perpendicular a r (o r') en el punto T, tal y como se justificó en el apartado Lugares geométricos.

El centro de la circunferencia buscada, solución de el problema, será la intersección de la recta perpendicular a r (o r') en el punto T con la bisectriz del ángulo formado por las rectas r y t.


Imagen:circunferencia_tangente_recta_punto_tangencia_recta.png



Circunferencias tangentes a una recta o una circunferencia en un punto dado de la misma y tangentes además a una circunferencia dada

es una cosa redonda y su fórmula es P2+K2y a+a2=KK[Imagen:circunferencias_tangentes_recta_punto_tangencia_circunferencia_dilatacion.png|center|500px]]

Obtenido de "http://www.wikillerato.org/Circunferencias_tangentes_conocido_el_punto_de_tangencia.html"
   
 
ASIGNATURAS
 MatemáticasFísicaQuímicaBiologíaDibujoHistoriaLengua y LiteraturaHistoria del ArteFilosofía
Creative Commons License
Los contenidos de Wikillerato están disponibles bajo una licencia de Creative Commons.
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.