Primitiva de una función
De Wikillerato
| Línea 7: | Línea 7: | ||
Su derivada que denotaremos por <math>g(x)</math> es: | Su derivada que denotaremos por <math>g(x)</math> es: | ||
| - | <math> g(x) = f' (x) = 2 x</math>, | + | <math> g(x) = f' (x) = 2 x \,</math>, |
| - | por lo que la primitiva de <math>g(x)</math> que denotaremos como <math>\int g(x)</math> es igual a: | + | por lo que la primitiva de <math>g(x) \,</math> que denotaremos como <math>\int g(x)\, </math> es igual a: |
| - | <math>\int g(x) = \int 2x = x^2 = f(x)</math>. | + | <math>\int g(x) = \int 2x = x^2 = f(x) \,</math>. |
Sin embargo, el resultado anterior es '''sólo''' parcialmente correcto. El problema es que la inversa de la derivada no es única. Si os dais cuenta, podemos sumar a f(x) una constante y su derivada no cambiará. | Sin embargo, el resultado anterior es '''sólo''' parcialmente correcto. El problema es que la inversa de la derivada no es única. Si os dais cuenta, podemos sumar a f(x) una constante y su derivada no cambiará. | ||
Revisión de 09:04 14 mar 2007
Calcular la primitiva de una función es el proceso inverso al de calcular su derivada.
Consideremos la función:
[Unparseable or potentially dangerous latex formula. Error 3 ].
Su derivada que denotaremos por [Unparseable or potentially dangerous latex formula. Error 3 ] es:
[Unparseable or potentially dangerous latex formula. Error 3 ],
por lo que la primitiva de [Unparseable or potentially dangerous latex formula. Error 3 ] que denotaremos como [Unparseable or potentially dangerous latex formula. Error 3 ] es igual a:
[Unparseable or potentially dangerous latex formula. Error 3 ].
Sin embargo, el resultado anterior es sólo parcialmente correcto. El problema es que la inversa de la derivada no es única. Si os dais cuenta, podemos sumar a f(x) una constante y su derivada no cambiará.
Por lo tanto si:
[Unparseable or potentially dangerous latex formula. Error 3 ],
tenemos que
[Unparseable or potentially dangerous latex formula. Error 3 ],
donde 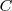 es una constante.
es una constante.



