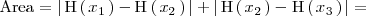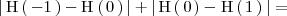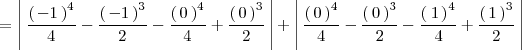Navegación
Cálculo de áreas y volúmenes
De Wikillerato
| Línea 164: | Línea 164: | ||
\left| \, \mathrm{H} \left( \, x_2 \, \right) - \mathrm{H} \left( | \left| \, \mathrm{H} \left( \, x_2 \, \right) - \mathrm{H} \left( | ||
\, x_3 \, \right) \, \right| = | \, x_3 \, \right) \, \right| = | ||
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
\left| \, \mathrm{H} \left( \, -1 \, \right) - \mathrm{H} \left( | \left| \, \mathrm{H} \left( \, -1 \, \right) - \mathrm{H} \left( | ||
\, 0 \, \right) \, \right| + | \, 0 \, \right) \, \right| + | ||
\left| \, \mathrm{H} \left( \, 0 \, \right) - \mathrm{H} \left( | \left| \, \mathrm{H} \left( \, 0 \, \right) - \mathrm{H} \left( | ||
\, 1 \, \right) \, \right| = | \, 1 \, \right) \, \right| = | ||
| - | \left| \, \frac{\left( \, -1 \, \right)^4}{4} - \frac{\left( \, -1 \, | + | </math> |
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = \left| \, \frac{\left( \, -1 \, \right)^4}{4} - \frac{\left( \, -1 \, | ||
\right)^3}{2} - \frac{\left( \, 0 \, \right)^4}{4} + \frac{\left( \, 0 \, | \right)^3}{2} - \frac{\left( \, 0 \, \right)^4}{4} + \frac{\left( \, 0 \, | ||
\right)^3}{2} \, \right| + | \right)^3}{2} \, \right| + | ||
Revisión de 11:04 25 dic 2010
Cálculo de áreas mediante integrales
Supongamos que nos dan dos funciones
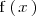y
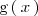y nos piden calcular el área comprendida entre las graficas de ambas
funciones.
El area que nos piden coincide con el área comprendida entre la función
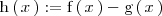y el eje X.
Para calcular el área comprendida entre la función
y el eje X, procedemos de la siguiente manera:
- 1. En primer lugar resolvemos la ecuación:
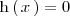
para obtener
soluciones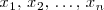 
con
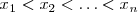
- 2 Buscamos una primitiva
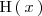de
.
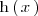- 3. Llegados a este punto ya podemos calcular el área que nos piden con la
fórmula:
donde
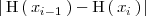
es el area comprendida entre las rectas verticales de ecuaciones
,
,
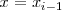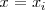el eje X y la grafica de la función
.
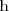Ejemplo
Calculemos el área comprendida entre las graficas de
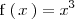y
.
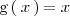El area que nos piden coincide con el área comprendida entre la función
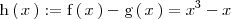y el eje X.
Para calcular el área comprendida entre la función
y el eje X, procedemos de la siguiente manera:
- 1. En primer lugar resolvemos la ecuación:
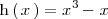
para obtener 3 soluciones
.
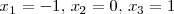- 2 Una primitiva
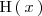de
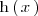es
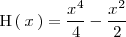
- 3. Llegados a este punto ya podemos calcular el área que nos piden:
