Integrales inmediatas
De Wikillerato
(Diferencias entre revisiones)
| Línea 3: | Línea 3: | ||
<br/> | <br/> | ||
| - | {| | + | |
| + | <center> | ||
| + | {| borders= "1" | ||
! Función <math>F \,\!</math>: primitiva de <math>f \,\!</math> | ! Función <math>F \,\!</math>: primitiva de <math>f \,\!</math> | ||
! función <math>f \,\!</math>: derivada de <math>F \,\!</math> | ! función <math>f \,\!</math>: derivada de <math>F \,\!</math> | ||
| Línea 41: | Línea 43: | ||
| <math>f'\left(x\right) = \frac{1}{1+x^2} \,\!</math> | | <math>f'\left(x\right) = \frac{1}{1+x^2} \,\!</math> | ||
|} | |} | ||
| + | </center> | ||
[[Category: Matemáticas]] | [[Category: Matemáticas]] | ||
Revisión de 17:22 15 nov 2010
Aquí están las principales funciones primitivas:
Función 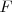 : primitiva de : primitiva de 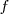
| función 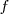 : derivada de : derivada de 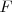
|
|---|---|
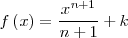
| [Unparseable or potentially dangerous latex formula. Error 3 ] |
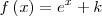
| 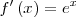
|
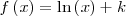
| 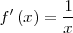
|
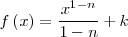
| 
|
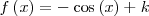
| 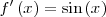
|
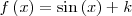
| 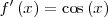
|
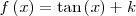
| 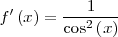
|
| [Unparseable or potentially dangerous latex formula. Error 3 ] | 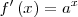
|
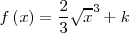
| 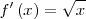
|
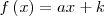
| 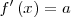
|
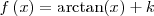
| 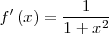
|



