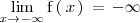Límite de una función
De Wikillerato
| Línea 52: | Línea 52: | ||
b | b | ||
</math> | </math> | ||
| - | de la recta real | + | de la recta real |
<math> | <math> | ||
| - | a, \, b \in \mathbb{R} | + | \left( |
| + | \, a, \, b \in \mathbb{R} \, | ||
| + | \right) | ||
</math> | </math> | ||
| - | + | es | |
<math> | <math> | ||
\left| \, a - b \, \right| | \left| \, a - b \, \right| | ||
| Línea 69: | Línea 71: | ||
b | b | ||
</math>. | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Por ejemplo, | ||
| + | <math> | ||
| + | -1 | ||
| + | </math> | ||
| + | esta mas cerca de | ||
| + | <math> | ||
| + | 2 | ||
| + | </math> | ||
| + | que el | ||
| + | <math> | ||
| + | 7 | ||
| + | </math> | ||
| + | ya que | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left| \, 2 - 7 \, \right| > \left| \, 2 - \left( -1 \right) \right| | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
==Limite de f(x) cuando x tiende a un número real== | ==Limite de f(x) cuando x tiende a un número real== | ||
| Línea 140: | Línea 166: | ||
x_0 | x_0 | ||
</math> | </math> | ||
| - | , por la derecha o por la izquierda. | + | , por la derecha o por la izquierda. |
<br/> | <br/> | ||
| Línea 160: | Línea 186: | ||
x_0 \in\mathbb{R} | x_0 \in\mathbb{R} | ||
</math> | </math> | ||
| - | existe y es igual a | + | por la '''''izquierda''''' existe y es igual a |
<math> | <math> | ||
\infty | \infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
</math> | </math> | ||
tan grande como queramos, eligiendo | tan grande como queramos, eligiendo | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | lo suficientemente cercano a | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | por la izquierda | ||
| + | <math> | ||
| + | \left( \, x_0 > x \, \right) | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Es decir | ||
| + | <center> | ||
| + | <math> | ||
| + | \forall y \in \mathbb{R}, \quad \exists \delta > 0 / | ||
| + | \left( | ||
| + | \, \mathrm{f} \left( \, x \, | ||
| + | \right) > y, \, \quad \forall x \in \left( \, x_0 - \delta, \, x_0 \, \right) | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Lo expresamos de la siguiente manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right) \, = \, \infty | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Analogamente, el límite de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | , cuando | ||
<math> | <math> | ||
x | x | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | x_0 \in\mathbb{R} | ||
| + | </math> | ||
| + | por la '''''derecha''''' existe y es igual a | ||
| + | <math> | ||
| + | \infty | ||
| + | </math> | ||
| + | si podemos hacer | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | tan grande como queramos, eligiendo | ||
| + | <math> | ||
| + | x | ||
</math> | </math> | ||
lo suficientemente cercano a | lo suficientemente cercano a | ||
<math> | <math> | ||
x_0 | x_0 | ||
| + | </math> | ||
| + | por la derecha | ||
| + | <math> | ||
| + | \left( \, x > x_0 \, \right) | ||
</math>. | </math>. | ||
| Línea 185: | Línea 274: | ||
\left( | \left( | ||
\, \mathrm{f} \left( \, x \, | \, \mathrm{f} \left( \, x \, | ||
| - | \right) > y, | + | \right) > y, \, \quad \forall x \in \left( \, x_0, \, x_0 + \delta \, \right) |
| - | + | ||
| - | \left( \, x_0, \, x_0 + \delta \, \right) | + | |
\right) | \right) | ||
</math> | </math> | ||
| Línea 198: | Línea 285: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \, = \, \infty | + | \lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right) \, = \, \infty |
</math> | </math> | ||
</center> | </center> | ||
| Línea 211: | Línea 298: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0} \frac{1}{x | + | \lim_{x \to 0^+} \frac{1}{x} = \infty |
</math> | </math> | ||
</center> | </center> | ||
| Línea 219: | Línea 306: | ||
y \in \mathbb{R} | y \in \mathbb{R} | ||
</math> | </math> | ||
| - | cualquiera e intentamos encontrar un | + | cualquiera e intentamos encontrar un |
| - | + | ||
<math> | <math> | ||
\delta > 0 | \delta > 0 | ||
</math> | </math> | ||
| - | + | de manera que | |
| - | de manera que | + | |
<center> | <center> | ||
<math> | <math> | ||
| - | x \in | + | x \in \left( \, 0, \, \delta \, \right) \Rightarrow \frac{1}{x} > y |
</math> | </math> | ||
</center> | </center> | ||
| Línea 236: | Línea 321: | ||
y | y | ||
</math> | </math> | ||
| - | no es positivo, entonces cualquier | + | no es positivo, entonces cualquier |
<math> | <math> | ||
\delta > 0 | \delta > 0 | ||
</math> | </math> | ||
| - | verifica | + | verifica |
<center> | <center> | ||
<math> | <math> | ||
| - | x \in | + | x \in \left( \, 0, \, \delta \, \right) \Rightarrow \frac{1}{x} > y |
| - | \Rightarrow \frac{1}{x | + | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 255: | Línea 339: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \frac{1}{x | + | \frac{1}{x} > y \Leftrightarrow \frac{1}{y} > x > 0 |
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 263: | Línea 346: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \delta = \frac{1} | + | \delta = \frac{1}{y} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 269: | Línea 352: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | x \in | + | x \in \left( \, 0, \, \delta \, \right) \Rightarrow \frac{1}{x} > y |
</math> | </math> | ||
</center> | </center> | ||
| Línea 291: | Línea 374: | ||
x_0 \in\mathbb{R} | x_0 \in\mathbb{R} | ||
</math> | </math> | ||
| - | existe y es igual a | + | por la '''''izquierda''''' existe y es igual a |
<math> | <math> | ||
-\infty | -\infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
</math> | </math> | ||
tan pequeño como queramos, eligiendo | tan pequeño como queramos, eligiendo | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | lo suficientemente cercano a | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | por la izquierda | ||
| + | <math> | ||
| + | \left( \, x_0 > x \, \right) | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Es decir | ||
| + | <center> | ||
| + | <math> | ||
| + | \forall y \in \mathbb{R}, \quad \exists \delta > 0 / | ||
| + | \left( | ||
| + | \, y > \mathrm{f} \left( \, x \, \right), \, \quad \forall x \in \left( \, x_0 - \delta, \, x_0 \, \right) | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Lo expresamos de la siguiente manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right) \, = \, -\infty | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Analogamente, el límite de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | , cuando | ||
<math> | <math> | ||
x | x | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | x_0 \in\mathbb{R} | ||
| + | </math> | ||
| + | por la '''''derecha''''' existe y es igual a | ||
| + | <math> | ||
| + | -\infty | ||
| + | </math> | ||
| + | si podemos hacer | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | tan pequeño como queramos, eligiendo | ||
| + | <math> | ||
| + | x | ||
</math> | </math> | ||
lo suficientemente cercano a | lo suficientemente cercano a | ||
<math> | <math> | ||
x_0 | x_0 | ||
| + | </math> | ||
| + | por la derecha | ||
| + | <math> | ||
| + | \left( | ||
| + | \, x > x_0 \, | ||
| + | \right) | ||
</math>. | </math>. | ||
| Línea 315: | Línea 462: | ||
\forall y \in \mathbb{R}, \quad \exists \delta > 0 / | \forall y \in \mathbb{R}, \quad \exists \delta > 0 / | ||
\left( | \left( | ||
| - | \, | + | \, \mathrm{f} \left( \, x \, \right) > y, \, \quad \forall x \in \left( \, x_0, \, x_0 + \delta \, \right) |
| - | \right), \, \quad \forall x \in | + | |
\right) | \right) | ||
</math> | </math> | ||
| Línea 327: | Línea 473: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \, = \, -\infty | + | \lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right) \, = \, -\infty |
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Cuando alguno de los limites laterales de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | cuando | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | es infinito o menos infinito, la grafica de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene una [[Asintotas#Asintotas verticales|asintota vertical]] de ecuación | ||
| + | <math> | ||
| + | x = x_0 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| Línea 435: | Línea 604: | ||
\infty | \infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
| Línea 490: | Línea 659: | ||
-\infty | -\infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
| Línea 626: | Línea 795: | ||
\infty | \infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
| Línea 681: | Línea 850: | ||
-\infty | -\infty | ||
</math> | </math> | ||
| - | + | si podemos hacer | |
<math> | <math> | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
Revisión de 21:08 18 ago 2010
Tabla de contenidos |
Nota sobre terminología
Utilizamos la palabra pequeño ( grande) de la siguiente manera:
 es mas pequeño ( grande ) que
es mas pequeño ( grande ) que
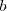 si y solo si
si y solo si
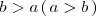 .
.
Es decir,
 es mas pequeño ( grande ) que
es mas pequeño ( grande ) que
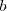 si
si
 es menor ( mayor ) que
es menor ( mayor ) que
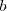 .
.
La distancia entre dos puntos
 y
y
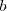 de la recta real
de la recta real
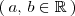 es
es
 .
Cuanto mas pequeña sea esta distancia mas proximos o
cercanos diremos que estan los puntos
.
Cuanto mas pequeña sea esta distancia mas proximos o
cercanos diremos que estan los puntos
 y
y
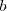 .
.
Por ejemplo,
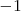 esta mas cerca de
esta mas cerca de
 que el
que el
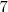 ya que
ya que

Limite de f(x) cuando x tiende a un número real
Limite finito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
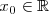 existe y es igual a
existe y es igual a
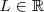 , si ambos límites laterales existen y son iguales a
, si ambos límites laterales existen y son iguales a
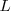 , es decir
, es decir
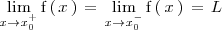
Lo expresamos de la siguiente manera:
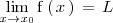
El que la anterior igualdad sea cierta significa que podemos hacer
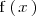 tan cercano a
tan cercano a
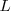 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
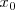 , por la derecha o por la izquierda.
, por la derecha o por la izquierda.
Limite infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
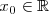 por la izquierda existe y es igual a
por la izquierda existe y es igual a
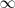 si podemos hacer
si podemos hacer
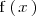 tan grande como queramos, eligiendo
tan grande como queramos, eligiendo
 lo suficientemente cercano a
lo suficientemente cercano a
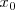 por la izquierda
por la izquierda
 .
.
Es decir
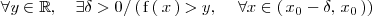
Lo expresamos de la siguiente manera:
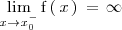
Analogamente, el límite de la función
 , cuando
, cuando
 tiende a
tiende a
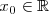 por la derecha existe y es igual a
por la derecha existe y es igual a
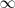 si podemos hacer
si podemos hacer
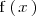 tan grande como queramos, eligiendo
tan grande como queramos, eligiendo
 lo suficientemente cercano a
lo suficientemente cercano a
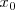 por la derecha
por la derecha
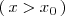 .
.
Es decir
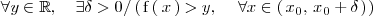
Lo expresamos de la siguiente manera:
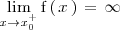
Ejemplo
Demostremos que
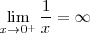
Para ello seleccionamos un
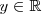 cualquiera e intentamos encontrar un
cualquiera e intentamos encontrar un
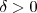 de manera que
de manera que
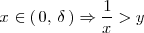
Si
 no es positivo, entonces cualquier
no es positivo, entonces cualquier
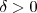 verifica
verifica
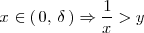
Si
 es positivo, entonces
es positivo, entonces
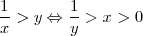
Por lo tanto, si elegimos
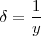
se verifica que
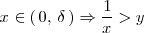
Limite menos infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
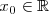 por la izquierda existe y es igual a
por la izquierda existe y es igual a
 si podemos hacer
si podemos hacer
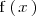 tan pequeño como queramos, eligiendo
tan pequeño como queramos, eligiendo
 lo suficientemente cercano a
lo suficientemente cercano a
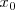 por la izquierda
por la izquierda
 .
.
Es decir
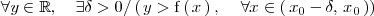
Lo expresamos de la siguiente manera:
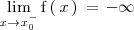
Analogamente, el límite de la función
 , cuando
, cuando
 tiende a
tiende a
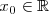 por la derecha existe y es igual a
por la derecha existe y es igual a
 si podemos hacer
si podemos hacer
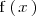 tan pequeño como queramos, eligiendo
tan pequeño como queramos, eligiendo
 lo suficientemente cercano a
lo suficientemente cercano a
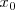 por la derecha
por la derecha
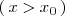 .
.
Es decir
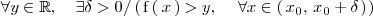
Lo expresamos de la siguiente manera:
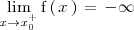
Cuando alguno de los limites laterales de
 cuando
cuando
 tiende a
tiende a
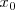 es infinito o menos infinito, la grafica de
es infinito o menos infinito, la grafica de
 tiene una asintota vertical de ecuación
tiene una asintota vertical de ecuación
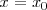 .
.
Limite de f(x) cuando x tiende a infinito
Limite finito
Se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
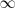 , es
, es
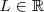 si cualquier sucesión
si cualquier sucesión
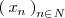 que tiende a
que tiende a
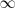 verifica que
verifica que
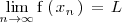 .
.
Lo expresamos como:
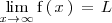
El que la anterior igualdad sea cierta significa que podemos hacer
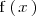 tan cercano a
tan cercano a
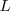 como queramos eligiendo
como queramos eligiendo
 lo suficientemente grande.
lo suficientemente grande.
Es decir
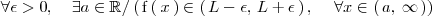
Limite infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
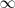 existe y es igual a
existe y es igual a
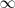 si podemos hacer
si podemos hacer
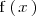 tan grande como queramos, eligiendo
tan grande como queramos, eligiendo
 lo suficientemente grande.
lo suficientemente grande.
Es decir
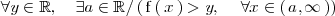
Lo expresamos de la siguiente manera:
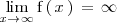
Limite menos infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
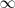 existe y es igual a
existe y es igual a
 si podemos hacer
si podemos hacer
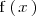 tan pequeño como queramos, eligiendo
tan pequeño como queramos, eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
Es decir
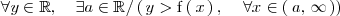
Lo expresamos de la siguiente manera:
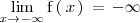
Limite de f(x) cuando x tiende a menos infinito
Limite finito
Se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
 , es
, es
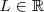 si cualquier sucesión
si cualquier sucesión
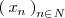 que tiende a
que tiende a
 verifica que
verifica que
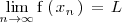 .
.
Lo expresamos como:
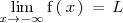
El que la anterior igualdad sea cierta significa que podemos hacer
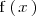 tan cercano a
tan cercano a
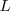 como queramos eligiendo
como queramos eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
Es decir
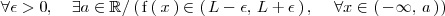
Limite infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
 existe y es igual a
existe y es igual a
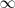 si podemos hacer
si podemos hacer
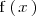 tan grande como queramos, eligiendo
tan grande como queramos, eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
Es decir
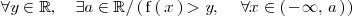
Lo expresamos de la siguiente manera:
Limite menos infinito
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
 existe y es igual a
existe y es igual a
 si podemos hacer
si podemos hacer
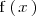 tan pequeño como queramos, eligiendo
tan pequeño como queramos, eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
Es decir
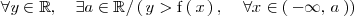
Lo expresamos de la siguiente manera: