Cuadriláteros
De Wikillerato
(→Cuadriláteros inscriptibles) |
|||
| Línea 157: | Línea 157: | ||
[[Imagen:DibujoTecnico_I-3_22.gif]] | [[Imagen:DibujoTecnico_I-3_22.gif]] | ||
| + | |||
| + | [[Categoría: Dibujo]] | ||
Revisión de 08:39 17 nov 2008
Características generales
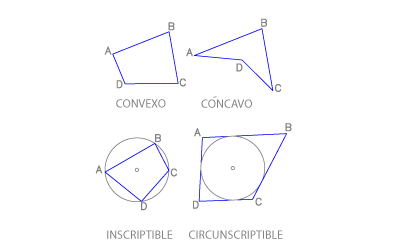
Un cuadrilátero ABCD es una figura plana limitada por cuatro lados y cuatro vértices. Puede ser cóncavo o convexo, inscriptible o circunscriptible.
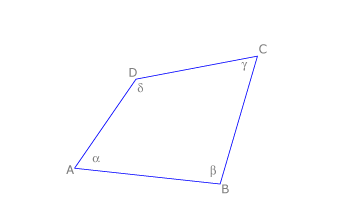
Nomenclatura
Recordamos que los cuadriláteros, como los demás polígonos se nombran por sus vértices, siguiendo el orden alfabético. Cada ángulo se nombra por la letra griega correspondiente al orden del alfabeto griego o indicando su vértice, como ya hemos visto al hablar de triángulos.
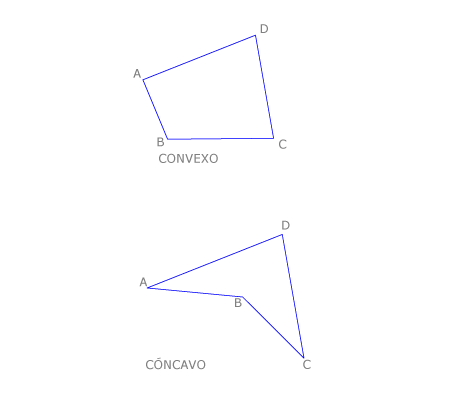
Cuadriláteros cóncavos o convexos
Recordamos que un polígono es convexo cuando no contiene prolongaciones de sus lados y es cóncavo cuando las contiene. Los ángulos internos de los cuadriláteros suman 360º, sean cóncavos o convexos, pues en ambos casos una diagonal los divide en dos triángulos.
Cuadriláteros idénticos, iguales y semejantes
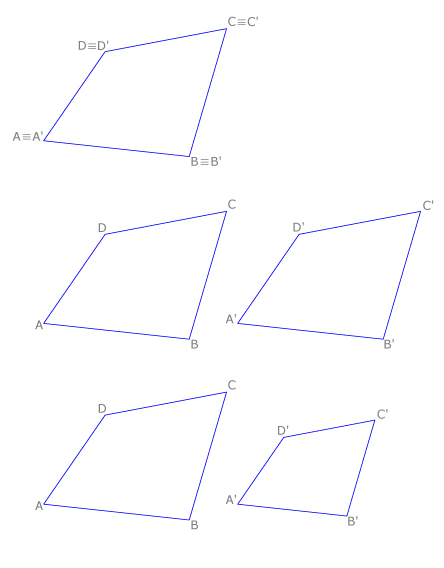
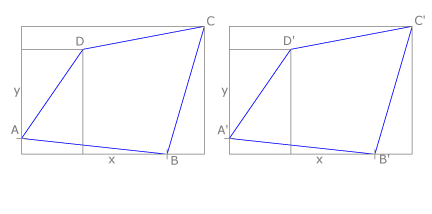
Un polígono es idéntico a otro cuando es igual y ocupa el mismo lugar. Como los cuadriláteros de la figura, ABCD ≡ A’B’C’D’.
Un polígono es igual a otro cuando sus lados y ángulos correspondientes son iguales con el mismo orden. En la figura ABCD = A’B’C’D’.
Un polígono es semejante a otro cuando sus lados son directamente proporcionales y sus ángulos correspondientes iguales, con el mismo orden.
En la figura ABCD es semejante a A’B’C’D’.
Cómo se dibujan polígonos iguales
Vamos a ver dos métodos de dibujar un polígono igual a otro.
Por triangulación
Se dibujan las diagonales necesarias para dividir el polígono en triángulos. En el caso de un cuadrilátero basta con trazar una diagonal. Se copian ordenadamente los triángulos obtenidos.
Por coordenadas
Se establece un sistema de ejes x e y. Se dibujan las coordenadas de los vértices ABCD respecto de tales ejes. Se repiten los ejes en el lugar donde se quiera dibujar el polígono igual y se llevan los datos de cada coordenada sobre ellos.
Cómo se dibujan polígonos semejantes
Para dibujar un cuadrilátero A’B’C’D’ semejante a ABCD, conociendo un lado A’B’, se superpone el lado conocido al correspondiente en el dato, haciendo coincidir un vértice A=A’. Se dibuja la diagonal AC que será común a ambas figuras. Por B’ se traza la paralela a BC, obteniendo C’. Por C’ se traza la paralela a CD, obteniendo D’.
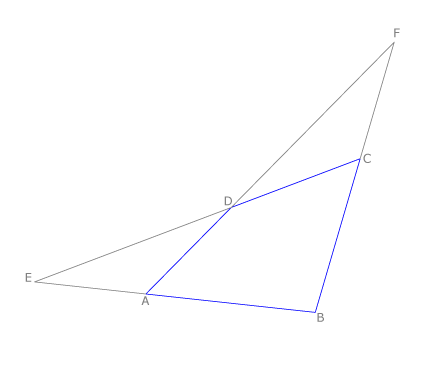
Cuadrilátero completo
Se llama así al obtenido por todas las intersecciones de sus lados ABCDEF.
Alturas y alturas medias de un cuadrilátero
Se llama altura a la distancia desde un vértice al lado opuesto. Si nos fijamos en la figura vemos que desde D se puede trazar otra altura perpendicular a BC, que también es lado opuesto. Por lo tanto, en los cuadriláteros y polígonos con más lados, este concepto solamente es interesante si se concreta el vértice y el lado a los que se refiere la altura.
Se llama altura media o semi-altura de un cuadrilátero a la recta perpendicular a un lado que pasa por el punto medio del lado opuesto.
Relaciones entre las diagonales y los lados de los cuadriláteros
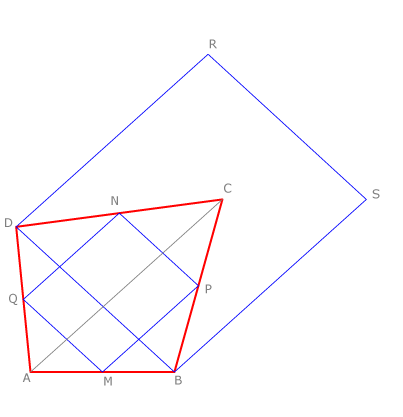
Si en un cuadrilátero ABCD trazamos por los extremos de la diagonal BD paralelas a la otra diagonal definimos un paralelogramo DBSR semejante al que se forma uniendo los puntos medios de cada lado, QMPN. Los lados de DBSR miden el doble que los correspondientes de QMPN. El resultado sería igual partiendo de la diagonal AC.
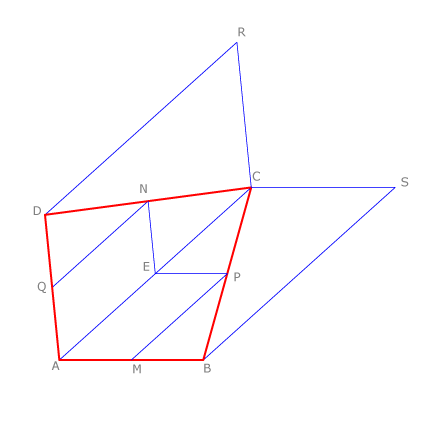
Si en un cuadrilátero ABCD trazamos por un extremo C de la diagonal AC rectas paralelas a los lados que pasan por A, definimos los paralelogramos ACRD y ABSC semejantes a AENQ y a AMPE, respectivamente. AENQ y AMPE son los paralelogramos obtenidos al unir los puntos medios de dos lados con el punto medio de la diagonal AC y el vértice A. Los lados de ACRD y ABSC miden el doble que los correspondientes de AENQ y AMPE.
Si partimos de la diagonal BD del mismo cuadrilátero obtendremos otros paralelogramos con las mismas relaciones de semejanza.
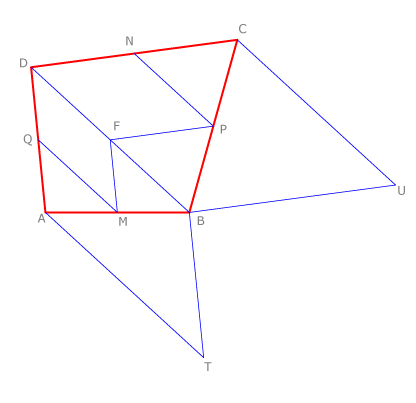
Si en un cuadrilátero ABCD unimos los puntos medios de las diagonales con los puntos medios de dos lados opuestos, como vemos en la figura, obtenemos un paralelogramo FMEN cuyos lados son paralelos al otro par de lados opuestos y miden la mitad que ellos.
También se definen:
dos cuadriláteros semejantes a ABCD con los lados paralelos o coincidentes a los suyos y que miden la mitad que ello, DQFN y NEPC. dos paralelogramos cuyos lados son paralelos o coincidentes con lados de ABCD midiendo la mitad que ellos, QAMF y MBPE.
Si unimos los puntos medios de las diagonales con los puntos medios del otro par de lados opuestos del mismo cuadrilátero obtendremos otros cuadriláteros con las mismas relaciones de semejanza.
Cuadriláteros inscriptibles
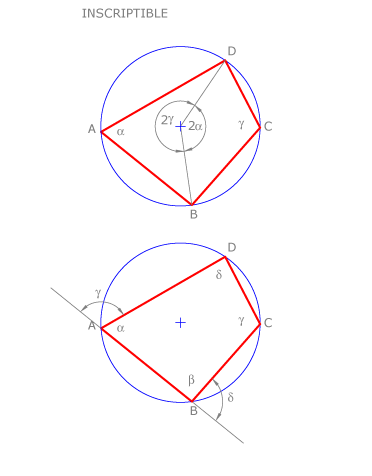
Un cuadrilátero es inscriptible cuando sus ángulos opuestos son suplementarios.
En la figura vemos el cuadrilátero ABCD inscrito en una circunferencia.
Sus vértices B y D definen los arcos DAB y BCD cuyos ángulos centrales suman 360º. Por lo tanto los ángulos inscritos correspondientes, 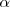 y
y 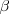 sumarán
El mismo razonamiento puede aplicarse a los vértices A y C.
sumarán
El mismo razonamiento puede aplicarse a los vértices A y C.
Teorema de Tolomeo
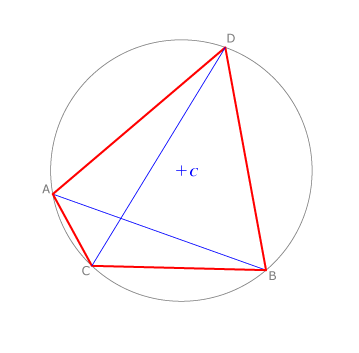
“Si ABCD es un cuadrilátero inscriptible se verifica que AB•CD+BC•DA=AC•BD”
Es decir, la suma de los productos de sus lados opuestos es igual al producto de sus diagonales.
Existe un caso particular muy interesante. Cuando ABD es un triángulo equilátero, para todo C perteneciente al arco AB, se verifica que: CD = CB+CA.
Centro de gravedad de un cuadrilátero inscriptible
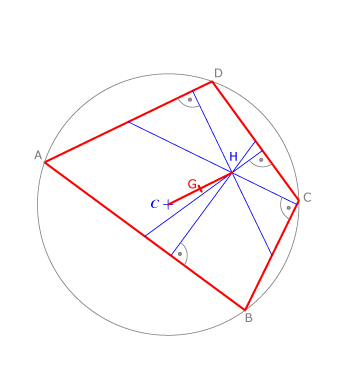
En un cuadrilátero incriptible el centro de gravedad está en la intersección de las rectas que unen los puntos medios de dos lados opuestos.
Se cumple que el punto de intersección de las alturas medias, H, y el centro de la circunferencia circunscrita, O, definen un segmento cuyo punto medio es el centro de gravedad, G.
Teorema japonés
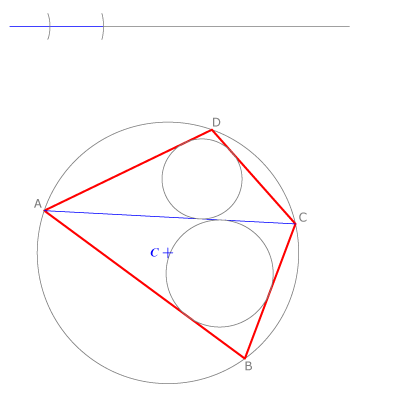
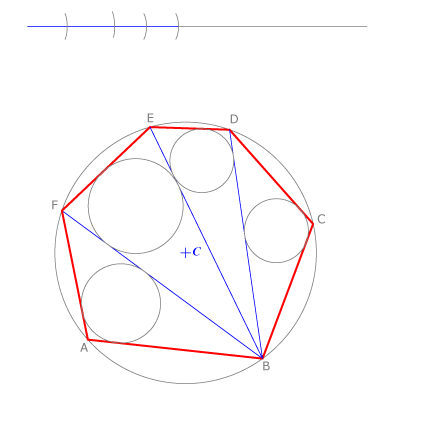
En un cuadrilátero inscriptible se verifica que la suma de los radios de las cirunferencias inscritas en los triángulos definidos por una diagonal es igual sea cual sea la diagonal considerada.
Este teorema es aplicable a cualquier polígono inscriptible.
Cuadriláteros circunscriptibles
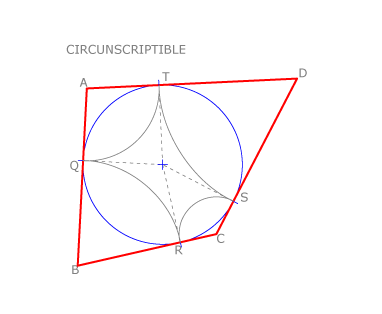
Un cuadrilátero es circunscriptible cuando las sumas de sus lados opuestos son iguales : AB+CD = AD+BC
Esta condición es muy fácil de comprobar, recordando que la circunferencia inscrita en un ángulo tiene los puntos de tangencia con los lados del ángulo equidistantes del vértice.
En la figura vemos que AT=AQ; BQ=BR; CR=CS y DT=DS.
Además: AB = AQ+BQ; CD = CS+DS; AD = AT+DT; BC = BR+CR;
Para verificar que AB+CD = AD+BC, se aplica lo anterior:
AB+CD = AQ+BQ +CS+DS;
AD+BC = AT+DT +BR+CR= AQ+BQ +CS+DS.
Tweet