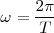Magnitudes características de una onda
De Wikillerato
| Línea 18: | Línea 18: | ||
Habrá que definir una nueva magnitud que es propia de las ondas y es su longitud de onda <math> \lambda</math>, que la volveremos a definir como la distancia entre dos puntos consecutivos que se encuentran en el mismo estado de vibración, lo que se dice en concordancia de fase. | Habrá que definir una nueva magnitud que es propia de las ondas y es su longitud de onda <math> \lambda</math>, que la volveremos a definir como la distancia entre dos puntos consecutivos que se encuentran en el mismo estado de vibración, lo que se dice en concordancia de fase. | ||
| - | + | [[Imagen:Magnitudesondas.png]] | |
<span style="text-decoration:underline">'''Recapitulando'''</span> | <span style="text-decoration:underline">'''Recapitulando'''</span> | ||
Revisión actual
Tal y como se ha señalado en lo presentado hasta ahora, si la causa que creó un pulso, repite su movimiento de un modo continuo se crea un tren de ondas.
¿Cuáles son las parámetros que nos van a ayudar a establecer una ecuación que nos permita determinar cómo han cambiado las propiedades que se modifican en el medio a consecuencia del paso de las ondas?
Hemos encontrado ya dos resultados:
a) En un medio homogéneo las ondas se propagan a velocidad constante.
b) En el caso de que no haya amortiguamiento, el pulso no se deforma. Por otra parte, consideraremos que los medios son lo suficientemente abiertos (una cuerda larga, un a superficie de agua indefinida, etc) como para que no se produzcan reflexiones que podrían entorpecer nuestro estudio.
Del apartado a) podremos utilizar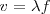 .
.
Del aparatado b), dado que no hay amortiguamiento, la amplitud 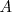 de las oscilaciones del foco emisor se mantiene constante, así como su periodo
de las oscilaciones del foco emisor se mantiene constante, así como su periodo 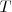 . A los puntos en donde la elongación es igual a la amplitud, por encima del nivel de la cuerda o de la superficie del agua, se les llama crestas y a aquellos que se encuentran por debajo se llaman valles.
. A los puntos en donde la elongación es igual a la amplitud, por encima del nivel de la cuerda o de la superficie del agua, se les llama crestas y a aquellos que se encuentran por debajo se llaman valles.
Pero además se mantendrán constantes la pulsación o frecuencia angular 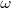 , la constante de fase
, la constante de fase 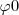 .
.
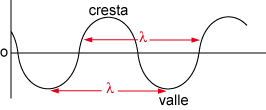
Habrá que definir una nueva magnitud que es propia de las ondas y es su longitud de onda 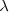 , que la volveremos a definir como la distancia entre dos puntos consecutivos que se encuentran en el mismo estado de vibración, lo que se dice en concordancia de fase.
, que la volveremos a definir como la distancia entre dos puntos consecutivos que se encuentran en el mismo estado de vibración, lo que se dice en concordancia de fase.
Recapitulando
Amplitud de las oscilaciones, A, o máxima distancia a la posición de equilibrio.
Elongación, y, distancia del punto a la posición de equilibrio en un instante.
Dado que son distancias, amplitud y elongación se miden en metros, m.
Frecuencia, f, o número de oscilaciones por segundo, se mide en hertzios, Hz.
Periodo, T, o tiempo que emplea el punto en describir una oscilación completa, se mide en segundos, s. El Periodo será la inversa de la frecuencia. 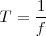
La longitud de onda, 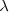 , o mínima distancia entre dos puntos del medio que se encuentren en igualdad de fase.
, o mínima distancia entre dos puntos del medio que se encuentren en igualdad de fase.
La pulsación o frecuencia angular 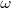 , siendo
, siendo