Rectas tangentes a dos circunferencias
De Wikillerato
(→Circunferencias interiores) |
m (Revertidas las ediciones realizadas por 87.218.66.77 (Talk); a la última edición de Jaimecarrion) |
||
| (23 ediciones intermedias no se muestran.) | |||
| Línea 42: | Línea 42: | ||
=== Circunferencias secantes === | === Circunferencias secantes === | ||
| + | |||
| + | Si dos circunferencias son secantes entonces únicamente poseen dos rectas tangentes comunes. Dichas tangentes comunes se corresponden con las tangentes exteriores, no existiendo tangentes interiores comunes a las circunferencias secantes. En efecto, si C y C' son los centros de dos circunferencias secantes, todos los puntos del segmento son interiores a ambas circunferencias y, en consecuencia, no se puede trazar ninguna tangente común a las circunferencias C y C' que pase por ellos. | ||
=== Circunferencias tangentes === | === Circunferencias tangentes === | ||
| + | |||
| + | Dos circunferencias tangentes exteriormente tendrán dos rectas tangentes exteriores comunes pero una única recta tangente interior común. La tangente interior común será perpendicular a la recta que une los centros de ambas circunferencias y pasará por el punto de tangencia de las dos circunferencias, siendo éste precisamente el punto de tangencia con una y otra circunferencia. | ||
| + | |||
| + | [[Imagen:tangentes_dos_circunferencias_tangentes_exteriormente.png]] | ||
| + | |||
| + | Dos circunferencias tangentes interiormente no tendrán ninguna recta tangente interior común (por la misma razón que las circunferencias interiores no tienen tangentes comunes) pero sí una única recta tangente exterior común. La tangente exterior común será perpendicular a la recta que une los centros de ambas circunferencias y pasará por el punto de tangencia de las dos circunferencias, siendo éste precisamente el punto de tangencia con una y otra circunferencia. | ||
| + | |||
| + | [[Imagen:tangentes_dos_circunferencias_tangentes_interiormente.png]] | ||
=== Circunferencias del mismo radio === | === Circunferencias del mismo radio === | ||
| + | |||
| + | Dos circunferencias del mismo radio presentan la particularidad de que las tangentes exteriores comunes a ambas circunferencias son paralelas entre sí y paralelas a la recta que une los centros de ambas circunferencias. Para trazar estas rectas tangentes no hay más que dibujar sendas rectas perpendiculares a la recta que une los centros de las circunferencias que pasen por los centros de una y otra circunferencia. Estas rectas perpendiculares cortarán a las circunferencias en los puntos de tangencia de las tangentes exteriores comunes a ambas circunferencias. | ||
| + | |||
| + | Si las circunferencias no son secantes tendrán además dos tangentes interiores comunes. Ambas tangentes interiores se cortarán justo en el punto medio del segmento cuyos extremos son los centros de las dos circunferencias. El problema de trazar las tangentes interiores comunes a dos circunferencias con el mismo radio se reduce por tanto a trazar las rectas tangentes a una u otra circunferencia desde el punto central del segmento cuyos extremos son los centros de ambas circunferencias. | ||
| + | |||
| + | [[Imagen:tangentes_dos_circunferencias_mismo_radio.png]] | ||
| + | |||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
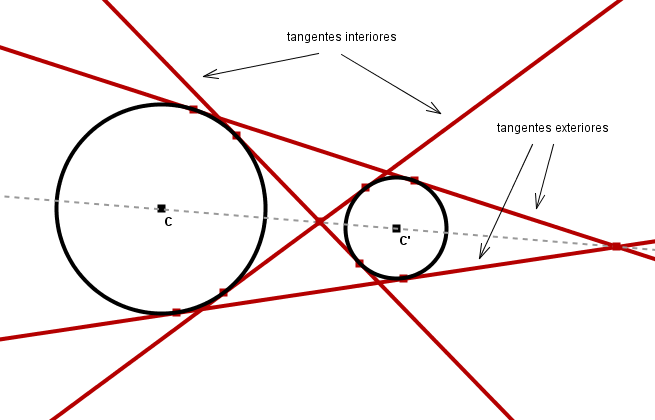
Dos circunferencias C y C' poseen, en general, cuatro rectas tangentes comunes. Dichas tangentes, así como los respectivos puntos de tangencia, son simétricas dos a dos respecto de la recta CC' que une los centros de las circunferencias. Cada par de tangentes simétricas se cortan en un punto de la recta CC'. En función de la ubicación de este punto se distingue entre tangentes interiores (cuando el punto de corte está situado entre los dos centros C y C') y tangentes exteriores (en el caso contrario) a las dos circunferencias. Estos puntos de corte de las tangentes simétricas no son otros que los centros de homotecia positiva y negativa de las circunferencias.
Si r es el radio de la circunferencia C y r' es el radio de la circunferencia C', entonces las rectas tangentes deben ser tales que estén a una distancia r del punto C y a una distancia r' del punto C', justificando la relación de simetría. Por otra parte, si r'<r y se traza una paralela a una recta tangente a una distancia r' de la misma de forma que pase por el centro C', su distancia al punto C será ahora r+r' o r-r', según que la paralela se aleje o se acerque al centro C. La recta paralela a una tangente común a dos circunferencias C y C' que pasa por el centro C' estará más próxima a C que la recta tangente si la tangente es exterior, y estará más alejada de C si la tangente es interior.
Esto nos brinda un método general para trazar las tangentes comunes a dos circunferencias, como se describirá en los siguientes epígrafes.
Tabla de contenidos |
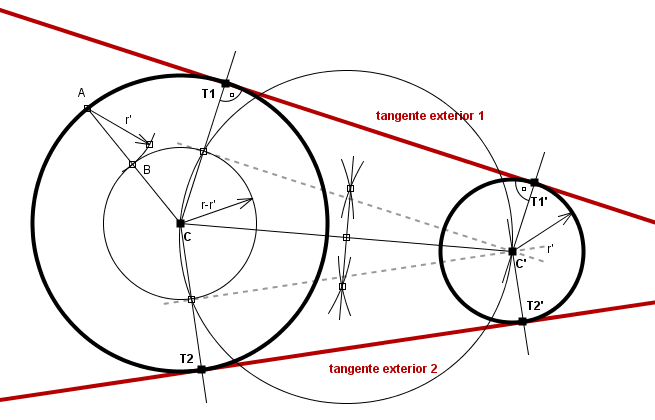
Trazado de las dos rectas tangentes exteriores comunes a dos circunferencias C y C'
Como se discutió anteriormente, si r es el radio de la circunferencia C y r' es el radio de la circunferencia C' y es r > r', entonces las rectas paralelas a las tangentes exteriores que pasan por C' estarán a una distancia del centro C igual a r-r' o, lo que es lo mismo, serán a su vez tangentes a una circunferencia de centro C y radio r-r'.
Los pasos para trazar las rectas tangentes exteriores a dos circunferencias C y C' de radios respectivos r y r', con r mayor que r', son:
- Trácese un radio de la circunferencia de centro C, que cortará a la propia circunferencia en un punto A de la misma.
- Con centro en el punto A, dibújese un arco de radio r', que cortará al radio antes trazado en un punto B interior a la circunferencia de centro C.
- Trácese la circunferencia con centro en C que pasa por el punto B, cuyo radio será r-r'.
- Hállense las rectas tangentes a la circunferencia de centro C y radio r-r' antes dibujada, trazadas desde el punto exterior C'.
- En las dos circunferencias C y C' trácense sendos radios perpendiculares a cada una de las tangentes obtenidas. Estos radios cortarán a la circunferencia correspondiente en los puntos de tangencia de las tangentes exteriores comunes a las dos circunferencias.
- Únanse las parejas de puntos de tangencia halladas para obtener las dos rectas tangentes exteriores comunes a las circunferencias C y C'.
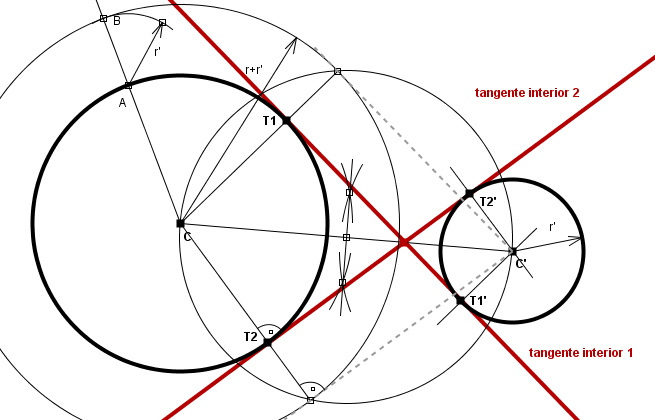
Trazado de las dos rectas tangentes interiores comunes a dos circunferencias C y C'
En este caso, las rectas paralelas a las tangentes interiores que pasan por C' van a ser a su vez tangentes a la circunferencia con centro en C y radio r+r'. Por lo tanto, los pasos para trazar las dos rectas tangentes interiores comunes a dos circunferencias C y C' de radios respectivos r y r' (r mayor que r') serán los siguientes:
- Dibújese un radio cualquiera de la circunferencia de centro C y sea el punto A el extremo de este radio situado sobre la circunferencia.
- Con centro en el punto A trácese un arco de radio igual al radio r' de la circunferencia C'; este arco cortará a la prolongación del radio antes dibujado en el punto B, exterior a la circunferencia de centro C.
- Dibújese la circunferencia con centro en C que pasa por el punto B, que tendrá un radio igual a r+r'.
- Trácense las rectas tangentes a la circunferencia de centro C y radio r+r' antes dibujada que pasan por el punto exterior C'.
- Trácense radios perpendiculares a cada una de las dos tangentes anteriores en ambas circunferencias. Los extremos de estos radios situados sobre las circunferencias serán los puntos de tangencia de las rectas tangentes interiores comunes con las correspondientes circunferencias.
- Únanse los puntos de antes hallados para obtener las correspondientes rectas tangentes interiores comunes a las circunferencias C y C'.
Casos particulares
Circunferencias interiores
Si una circunferencia es interior a otra (todos los puntos de la circunferencia pequeña están situados en el interior de la circunferencia grande), ambas circunferencias no poseen ninguna recta tangente común, ni interior ni exterior. Todas las rectas tangentes a la circunferencia interior serán secantes a la circunferencia que la contiene.
Circunferencias secantes
Si dos circunferencias son secantes entonces únicamente poseen dos rectas tangentes comunes. Dichas tangentes comunes se corresponden con las tangentes exteriores, no existiendo tangentes interiores comunes a las circunferencias secantes. En efecto, si C y C' son los centros de dos circunferencias secantes, todos los puntos del segmento son interiores a ambas circunferencias y, en consecuencia, no se puede trazar ninguna tangente común a las circunferencias C y C' que pase por ellos.
Circunferencias tangentes
Dos circunferencias tangentes exteriormente tendrán dos rectas tangentes exteriores comunes pero una única recta tangente interior común. La tangente interior común será perpendicular a la recta que une los centros de ambas circunferencias y pasará por el punto de tangencia de las dos circunferencias, siendo éste precisamente el punto de tangencia con una y otra circunferencia.
Dos circunferencias tangentes interiormente no tendrán ninguna recta tangente interior común (por la misma razón que las circunferencias interiores no tienen tangentes comunes) pero sí una única recta tangente exterior común. La tangente exterior común será perpendicular a la recta que une los centros de ambas circunferencias y pasará por el punto de tangencia de las dos circunferencias, siendo éste precisamente el punto de tangencia con una y otra circunferencia.
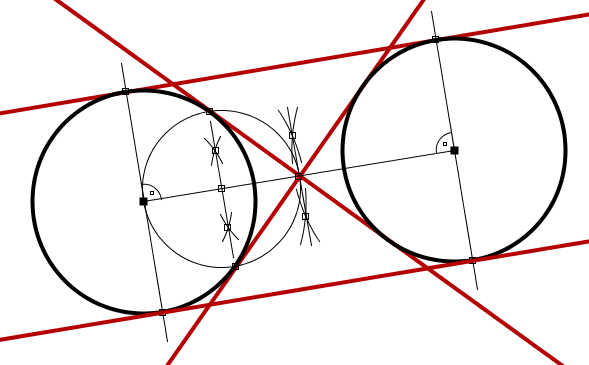
Circunferencias del mismo radio
Dos circunferencias del mismo radio presentan la particularidad de que las tangentes exteriores comunes a ambas circunferencias son paralelas entre sí y paralelas a la recta que une los centros de ambas circunferencias. Para trazar estas rectas tangentes no hay más que dibujar sendas rectas perpendiculares a la recta que une los centros de las circunferencias que pasen por los centros de una y otra circunferencia. Estas rectas perpendiculares cortarán a las circunferencias en los puntos de tangencia de las tangentes exteriores comunes a ambas circunferencias.
Si las circunferencias no son secantes tendrán además dos tangentes interiores comunes. Ambas tangentes interiores se cortarán justo en el punto medio del segmento cuyos extremos son los centros de las dos circunferencias. El problema de trazar las tangentes interiores comunes a dos circunferencias con el mismo radio se reduce por tanto a trazar las rectas tangentes a una u otra circunferencia desde el punto central del segmento cuyos extremos son los centros de ambas circunferencias.
Tweet