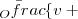Efecto Doppler
De Wikillerato
| Línea 47: | Línea 47: | ||
Si el observador hubiera permanecido en reposo, en un tiempo t habría recibido todas las ondas comprendidas en el segmento x = v t, ese número es | Si el observador hubiera permanecido en reposo, en un tiempo t habría recibido todas las ondas comprendidas en el segmento x = v t, ese número es | ||
| - | <math>\frac{x}{ | + | <math> \frac{x}{\lambda} = \frac{\nu t}{\lambda}</math> |
| - | Pero el observador se ha alejado una distancia | + | Pero el observador se ha alejado una distancia <math>x_o = v_o t</math>, llegando hasta el punto <math>C</math> y sólo percibirá las ondas comprendidas entre <math>B</math> y <math>O</math>, es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse. |
| - | <math> \frac{ | + | <math>\frac{\nu}{\lambda '} = \frac {\nu - \nu_o}{\lambda}</math> |
| - | <math> \frac{1}{ | + | <math> \frac{1}{\lambda '} = \frac {\nu - \nu_o}{\nu} \frac {1}{\lambda}</math> |
| - | + | <math> \f_o = \frac {\nu-\nu_o}{\nu} f </math> | |
Frecuencia percibida fO < f frecuencia de las ondas emitidas | Frecuencia percibida fO < f frecuencia de las ondas emitidas | ||
Revisión de 15:21 26 feb 2008
El efecto Doppler es un fenómeno común a todos los movimientos ondulatorios, aunque su observación es particularmente fácil en las ondas sonoras y en las ondas electromagnéticas, como se verá en su lugar. El fenómeno se observará en tanto la velocidad del foco emisor sea muy pequeña frente a la velocidad de propagación de las ondas.
Hasta ahora hemos supuesto que tanto el foco emisor como el observador se encontraban permanentemente en reposo así como el medio en el que se producen las ondas. Sin embargo, en un instante o intervalo de tiempo determinado, pueden encontrarse en movimiento uno, dos o los tres. La consecuencia de cualquiera de estos posibles movimientos es un cambio de frecuencia de las ondas percibidas por el observador.
Estudio Analítico
Foco emisor en movimiento, observador y medio en reposo
Supongamos que un foco emisor F, que emite ondas cuya velocidad de propagación es v, se mueve con respecto al observador O con una velocidad 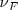 . Consideremos positivas las velocidades si se mueven hacia el observador y negativas si lo hacen en sentido contrario.
. Consideremos positivas las velocidades si se mueven hacia el observador y negativas si lo hacen en sentido contrario.
En un tiempo 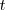 , la onda recorre una longitud
, la onda recorre una longitud 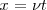 , acercándose al observador hasta el punto
, acercándose al observador hasta el punto 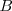 .
.
Si el foco emisor 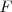 se acerca, durante ese mismo tiempo
se acerca, durante ese mismo tiempo 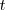 se ha desplazado
se ha desplazado 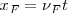 , llegando hasta el punto
, llegando hasta el punto 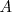 .
.
Durante ese tiempo 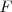 ha emitido un número de ondas igual a
ha emitido un número de ondas igual a 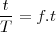 .
.
Estas ondas se encuentran comprimidas dentro de la distancia 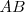 , y la distancia entre las ondas será la longitud de onda aparente
, y la distancia entre las ondas será la longitud de onda aparente 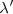 de las ondas percibidas por el observador.
de las ondas percibidas por el observador.
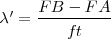 =
= 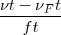 =
= 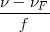
Pero la ecuación 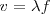 , se cumplirá siempre, en este caso, si es
, se cumplirá siempre, en este caso, si es 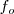 la frecuencia de las ondas percibida por el observador tendremos
la frecuencia de las ondas percibida por el observador tendremos 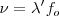 , con lo cual,
, con lo cual,
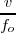 =
= 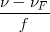
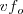 =
= 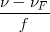
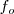 =
= 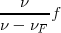
Frecuencia percibida  Frecuencia de las ondas emitidas
Frecuencia de las ondas emitidas
 disminuye la longitud de onda aparente.
disminuye la longitud de onda aparente.
Si el foco emisor se aleja del observador, su velocidad 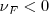 puesto que su velocidad tendrá sentido contrario al de las ondas que llegan al observador.
puesto que su velocidad tendrá sentido contrario al de las ondas que llegan al observador.
Cambiando el signo de 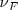 tendremos,
tendremos,
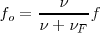
Frecuencia percibida  Frecuencia emitida.
Frecuencia emitida.
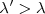 aumenta la longitud de onda aparente.
aumenta la longitud de onda aparente.
Observador en movimiento, foco emisor y medio en reposo
Si el observador se moviera con una velocidad vO alejándose del foco emisor F, la distancia entre los frentes de onda no se altera, sin embargo, el número de frentes que percibe en un tiempo t es menor, por lo cual la frecuencia aparente disminuye. Si el observador hubiera permanecido en reposo, en un tiempo t habría recibido todas las ondas comprendidas en el segmento x = v t, ese número es
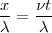
Pero el observador se ha alejado una distancia 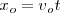 , llegando hasta el punto
, llegando hasta el punto 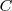 y sólo percibirá las ondas comprendidas entre
y sólo percibirá las ondas comprendidas entre 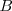 y
y 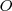 , es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse.
, es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse.
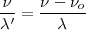
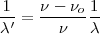
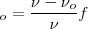
Frecuencia percibida fO < f frecuencia de las ondas emitidas
La longitud de onda aparente λ´>λ longitud de onda de las ondas emitidas
Si el observador se acerca al foco emisor, el número de frentes que percibe es mayor que si permaneciera en reposo. Para los cálculos basta cambiar de signo a la velocidad del observador vO puesto que O se mueve en sentido contrario al del movimiento del frente de ondas que le llega.