Ángulo doble y ángulo mitad
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | Como se explica en la sección sobre | + | Como se explica en la sección sobre las [[Razones trigonométricas de la suma y diferencia de ángulos|razones trigonométricas de la suma y diferencia de ángulos]]: |
| - | de ángulos| | + | |
<br/> | <br/> | ||
| Línea 52: | Línea 51: | ||
\mathrm{cos} | \mathrm{cos} | ||
\left( | \left( | ||
| - | \, \ | + | \, 2 \cdot \alpha \, |
\right) | \right) | ||
\, = \, \mathrm{cos} | \, = \, \mathrm{cos} | ||
| Línea 67: | Línea 66: | ||
\left( | \left( | ||
\, \alpha \, | \, \alpha \, | ||
| - | + | \right) | |
| - | + | ^2 | |
| + | \right) | ||
| + | \, = \, 2 \cdot \mathrm{cos} | ||
\left( | \left( | ||
\, \alpha \, | \, \alpha \, | ||
\right) | \right) | ||
\right) | \right) | ||
| - | \, = \, | + | ^2 \, - \, 1 |
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Según lo que se explica en la sección [[Razones trigonométricas de la suma y diferencia | ||
| + | de ángulos|razones trigonométricas de la suma y diferencia de ángulos]], se tiene que: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{sen} | ||
| + | \left( | ||
| + | \, \alpha \, + \alpha \, | ||
| + | \right) | ||
| + | \, = \, \mathrm{sen} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | \cdot \mathrm{cos} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | \, + \, | ||
\mathrm{cos} | \mathrm{cos} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | \cdot \mathrm{sen} | ||
\left( | \left( | ||
\, \alpha \, | \, \alpha \, | ||
| - | |||
\right) | \right) | ||
| - | + | \, = \, 2 \cdot \mathrm{sen} | |
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | \cdot \mathrm{cos} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
</math> | </math> | ||
</center> | </center> | ||
Revisión de 14:06 10 ene 2007
Como se explica en la sección sobre las razones trigonométricas de la suma y diferencia de ángulos:
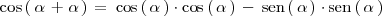
Teniendo en cuenta que
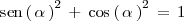 , deducimos que:
, deducimos que:
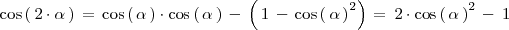
Según lo que se explica en la sección [[Razones trigonométricas de la suma y diferencia de ángulos|razones trigonométricas de la suma y diferencia de ángulos]], se tiene que: