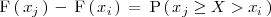Distribuciones discretas
De Wikillerato
| Línea 108: | Línea 108: | ||
\, = \, \frac{3}{8} | \, = \, \frac{3}{8} | ||
\qquad | \qquad | ||
| + | \\ | ||
| + | & | ||
\\ | \\ | ||
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P} | \mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P} | ||
| Línea 168: | Línea 170: | ||
La función de distribución de cualquier variable aleatoria discreta tiene las siguentes | La función de distribución de cualquier variable aleatoria discreta tiene las siguentes | ||
caracteristicas: | caracteristicas: | ||
| + | |||
| + | <br/> | ||
1. Al ser una probabilidad, | 1. Al ser una probabilidad, | ||
<math> | <math> | ||
| - | 1 \ge \mathrm{F} \ | + | 1 \ge \mathrm{F} \leg2 \, x_i \, \right) \ge 0 |
</math> | </math> | ||
. | . | ||
| Línea 256: | Línea 260: | ||
\, x_j \ge X > x_i \, | \, x_j \ge X > x_i \, | ||
\right) | \right) | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
</math> | </math> | ||
Revisión de 23:23 26 dic 2006
Tabla de contenidos |
Función de probabilidad
Denotaremos como
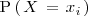 a la probabilidad de que la variable aleatoria tome el valor
a la probabilidad de que la variable aleatoria tome el valor
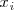 .
.
Se llama función de probabilidad de una variable aleatoria discreta
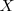 a la aplicacion que a cada valor de
a la aplicacion que a cada valor de
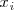 de la variable le hace corresponder la probabilidad de que la variable tome dicho
valor:
de la variable le hace corresponder la probabilidad de que la variable tome dicho
valor:
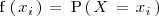
Por definición, deducimos que si
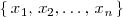 son los valores que puede tomar la variable
son los valores que puede tomar la variable
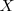 , entonces:
, entonces:
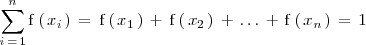
ya que esta suma es, en realidad, la probabilidad del suceso seguro.
Ejemplo
En el experimento de lanzar tres monedas al aire, la aplicación
 que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso:
que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso:
![\begin{array}[c]{cc}
\mathrm{f} \left( \, 0 \, \right) \, = \, \mathrm{P}
</p>
<pre>\left(
\, X \, = \, 0 \,
\right)
\, = \, \frac{1}{8} \qquad
&
\mathrm{f}
\left(
\, 1 \,
\right)
\, = \, \mathrm{P}
\left(
\, X \, = \, 1 \,
\right)
\, = \, \frac{3}{8}
\qquad
\\
&
\\
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 2 \,
\right)
\, = \, \frac{3}{8} \qquad
&
\mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 3 \,
\right)
\, = \, \frac{1}{8} \qquad
</pre>
<p>\end{array}
\begin{array}[c]{cc}
\mathrm{f} \left( \, 0 \, \right) \, = \, \mathrm{P}
</p>
<pre>\left(
\, X \, = \, 0 \,
\right)
\, = \, \frac{1}{8} \qquad
&
\mathrm{f}
\left(
\, 1 \,
\right)
\, = \, \mathrm{P}
\left(
\, X \, = \, 1 \,
\right)
\, = \, \frac{3}{8}
\qquad
\\
&
\\
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 2 \,
\right)
\, = \, \frac{3}{8} \qquad
&
\mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 3 \,
\right)
\, = \, \frac{1}{8} \qquad
</pre>
<p>\end{array}](/images/math/math-1e852aaf55786c2f933fe0d945c43f51.png)
Observa que
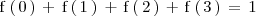
Función de distribución
Dada una variable aleatoria discreta
 , su función de distribución es la aplicación que a cada valor de
, su función de distribución es la aplicación que a cada valor de
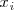 de la variable le asigna la probabilidad de que ésta tome valores menores o
iguales que
de la variable le asigna la probabilidad de que ésta tome valores menores o
iguales que
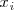 , y la denotamos por:
, y la denotamos por:
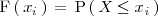
La función de distribución de cualquier variable aleatoria discreta tiene las siguentes caracteristicas:
1. Al ser una probabilidad,
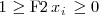 .
.
2.
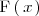 es nula para todo valor de
es nula para todo valor de
 menor que el menor valor de la variable aleatoria, y es igual a la unidad para
todo valor de
menor que el menor valor de la variable aleatoria, y es igual a la unidad para
todo valor de
 mayor que el mayor valor de la variable.
mayor que el mayor valor de la variable.
3.
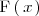 es creciente.
es creciente.
4.
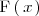 es constante en cada intervalo
es constante en cada intervalo
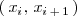 , además es continua a la derecha de
, además es continua a la derecha de
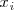 y a la izquierda
y a la izquierda
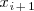 , y discontinua a la izquierda de
, y discontinua a la izquierda de
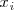 y a la derecha de
y a la derecha de
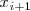 , para
, para

5. Sea
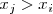 , entonces
, entonces