Matriz transpuesta
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 79.154.253.11 (Talk); a la última edición de Laura.2mdc) |
m (Revertidas las ediciones realizadas por 201.144.51.41 (Talk); a la última edición de Jaimecarrion) |
||
| (24 ediciones intermedias no se muestran.) | |||
| Línea 75: | Línea 75: | ||
\left( | \left( | ||
\begin{array}[c]{ccc} | \begin{array}[c]{ccc} | ||
| - | + | 1 & 2 & 3 | |
\\ | \\ | ||
| - | 2 & | + | 2 & 5 & 4 |
\\ | \\ | ||
| - | + | 3 & 4 & 6 | |
\end{array} | \end{array} | ||
\right) | \right) | ||
Revisión actual
Tabla de contenidos |
Definición
Se llama matriz traspuesta de una matriz
 de dimensión
de dimensión
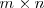 , a la matriz que se obtiene al cambiar en
, a la matriz que se obtiene al cambiar en
 las filas por columnas o las columnas por filas. Se representa por
las filas por columnas o las columnas por filas. Se representa por
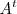 y su dimensión es
y su dimensión es

Propiedades
-
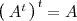
-
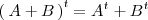
-
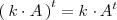
-
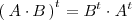
Matriz simétrica
Se llama matriz simétrica a toda matriz cuadrada
 que coincide con su transpuesta:
que coincide con su transpuesta:
 .
En una matriz simétrica cualquier par de elementos simétricos respecto a la
diagonal principal son iguales.
.
En una matriz simétrica cualquier par de elementos simétricos respecto a la
diagonal principal son iguales.
Ejemplo
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 5 & 4
\\
3 & 4 & 6
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 5 & 4
\\
3 & 4 & 6
\end{array}
</pre>
<p>\right)](/images/math/math-77a39010f0db3505fd7b42155bd88227.png)
Matriz antisimétrica
Se llama matriz antisimétrica a toda matriz cuadrada
 que coincide con la opuesta de su transpuesta:
que coincide con la opuesta de su transpuesta:
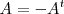 .
En una matriz simetrica cualquier par de elementos simétricos respecto a la
diagonal principal son opuestos.
.
En una matriz simetrica cualquier par de elementos simétricos respecto a la
diagonal principal son opuestos.
Ejemplo
![\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)](/images/math/math-790d68307dd50a5291399ef733c5b199.png)
Tweet
-
-
-



