Posiciones relativas de dos planos
De Wikillerato
| Línea 29: | Línea 29: | ||
Sean dos planos | Sean dos planos | ||
<math> | <math> | ||
| - | \ | + | \p21 |
</math> | </math> | ||
y | y | ||
| Línea 145: | Línea 145: | ||
Rango ( A ) = Rango ( A | B ) = 2 | Rango ( A ) = Rango ( A | B ) = 2 | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ---- | ||
<br/> | <br/> | ||
| Línea 192: | Línea 196: | ||
Rango ( A ) = Rango ( A | B ) = 1 | Rango ( A ) = Rango ( A | B ) = 1 | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ---- | ||
<br/> | <br/> | ||
Revisión de 18:17 18 dic 2006
Dos planos pueden adoptar tres posiciones relativas en el espacio:
1. Secantes.
2. Coincidentes.
3. Paralelos.
Sean dos planos
[Unparseable or potentially dangerous latex formula. Error 3 ]
y
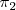 de ecuaciones:
de ecuaciones:
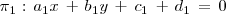
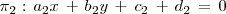
Para determinar sus posiciones relativas, analizamos el sistema formado por las ecuaciones de los dos planos, cuyas matrices asociadas son:
[Unparseable or potentially dangerous latex formula. Error 3 ]
[Unparseable or potentially dangerous latex formula. Error 3 ]
Según el teorema de Rouché-Frobenius, se pueden presentar los siguientes casos:
Caso 1: Rango ( A ) = Rango ( A | B ) = 2
El sistema de ecuaciones es compatible indeterminado y tiene infinitas soluciones. Los planos se cortan según una recta. Son planos secantes.
Asi, los planos
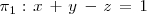
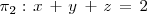
son secantes, pues:
Rango ( A ) = Rango ( A | B ) = 2
Caso 2: Rango ( A ) = Rango ( A | B ) = 1
El sistema de ecuaciones es compatible indeterminado, siendo la segunda ecuación proporcional a la primera. Los planos tienen en comun todos sus puntos. Son planos coincidentes.
Asi, los planos
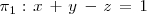
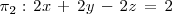
son coincidentes, pues:
Rango ( A ) = Rango ( A | B ) = 1
Caso 3: Rango ( A ) = Rango ( A | B ) = 2
El sistema de ecuaciones es incompatible, no tiene solucion. Los planos no tienen ningun punto en común. Son planos paralelos.
Asi, los planos
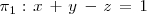
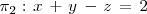
son paralelos, pues:
Rango ( A ) = 1 mientras que Rango ( A | B ) = 2



