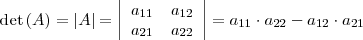|
|
| Línea 1: |
Línea 1: |
| - | ==Definición de matriz==
| + | A una matriz cuadrada le podemos asociar un número que, como veremos con posterioridad, |
| | + | nos permitirá estudiar y resolver un sistema de ecuaciones lineales y examinar si una |
| | + | matriz dada posee matriz inversa y calcularla. |
| | | | |
| - | <br/>
| + | Este número que vamos a asociar a una matriz cuadrada lo llamaremos determinante de dicha |
| | + | matriz. Veamos su calculo para matrices cuadradas de orden 2, y con posterioridad |
| | + | calcularemos determinantes de matrices cuadradas de cualquier orden. |
| | | | |
| - | Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension
| + | Para una matriz cuadrada de orden 2, |
| - |
| + | |
| - | <math>
| + | |
| - | m \times n
| + | |
| - | </math>
| + | |
| - | a un conjunto de números reales dispuestos en
| + | |
| - | <math>
| + | |
| - | m
| + | |
| - | </math>
| + | |
| - | filas y
| + | |
| - | <math>
| + | |
| - | n
| + | |
| - | </math>
| + | |
| - | columnas de la siguiente forma
| + | |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | <center>
| + | |
| | <math> | | <math> |
| | + | A = |
| | \left( | | \left( |
| - | \begin{array}[c]{cccc} | + | \begin{array}[c]{cc} |
| - | a_{11 }& a_{12} & \ldots & a_{1n} | + | a_{11} & a_{12} |
| | \\ | | \\ |
| - | a_{21 }& a_{22} & \ldots & a_{2n} | + | a_{21} & a_{22} |
| - | \\
| + | |
| - | \vdots & \vdots & \ddots & \vdots
| + | |
| - | \\
| + | |
| - | a_{m1 }& a_{m2} & \ldots & a_{mn}
| + | |
| | \end{array} | | \end{array} |
| | \right) | | \right) |
| | </math> | | </math> |
| - | </center>
| + | se llama determinante de |
| - | | + | |
| - | <br/>
| + | |
| - | | + | |
| - | La matriz
| + | |
| | <math> | | <math> |
| - | A | + | A |
| | </math> | | </math> |
| - | se puede designar tambien como | + | al número real: |
| - | <math>
| + | |
| - | \quad A = \left( a_{ij} \right) \quad
| + | |
| - | </math>
| + | |
| - | donde
| + | |
| | | | |
| | <br/> | | <br/> |
| Línea 52: |
Línea 28: |
| | <center> | | <center> |
| | <math> | | <math> |
| - | \left\{ | + | \makebox{det} \left( A \right) = \left| A \right| = |
| - | \begin{array}[c]{l} | + | \left| |
| - | i = 1, \, 2, \, \ldots, \, m | + | \begin{array}{cc} |
| | + | a_{11} & a_{12} |
| | \\ | | \\ |
| - | j = 1, \, 2, \, \ldots, \, n | + | a_{21} & a_{22} |
| | \end{array} | | \end{array} |
| - | \right. | + | \right| |
| | + | = a_{11} \cdot a_{22} - a_{12} \cdot a_{21} |
| | </math> | | </math> |
| | </center> | | </center> |
| | | | |
| | <br/> | | <br/> |
| - |
| |
| - | Un elemento generico de la matriz se designa por
| |
| - | <math>
| |
| - | a_{ij}
| |
| - | </math>
| |
| - | en el cual el subindice
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | representa el numero de fila que ocupa el elemento y el subindice
| |
| - | <math>
| |
| - | j
| |
| - | </math>
| |
| - | el numero de columna.
| |
| - |
| |
| - | El conjunto de matrices de dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | se denota por:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | M_{m \times n}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | El conjunto de matrices de dimension
| |
| - | <math>
| |
| - | n \times n
| |
| - | </math>
| |
| - | , tambien llamadas de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | , se denota por:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | M_n
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
| |
| - |
| |
| - | * la diagonal principal formada por los elementos de la forma
| |
| - | <math>
| |
| - | a_{ii}
| |
| - | </math>
| |
| - |
| |
| - |
| |
| - | *la diagonal secundaria formada por los elementos de la forma
| |
| - | <math>
| |
| - | a_{ij}
| |
| - | </math>
| |
| - | tales que
| |
| - | <math>
| |
| - | i + j = n + 1
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | [[Image:diagonales.gif]]
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Una '''matriz rectangular''' es aquella que tiene distinto número de filas que de columnas
| |
| - |
| |
| - | <math>
| |
| - | \left(
| |
| - | m \neq n
| |
| - | \right)
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz rectangular====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & -1 & ~~0
| |
| - | \\
| |
| - | 2 & ~~3 & -1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz fila''' es toda matriz rectangular con una sola fila de dimension
| |
| - | <math>
| |
| - | 1 \times n
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz fila====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | -1 & 3 & 5
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ''''Matriz columna'''' es toda matriz rectangular con una sola columna de dimension
| |
| - | <math>
| |
| - | m \times 1
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz columna====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{c}
| |
| - | -1
| |
| - | \\
| |
| - | ~~3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Una '''matriz nula''' es una matriz rectangular con todos sus elementos nulos. Se denota
| |
| - | por
| |
| - | <math>
| |
| - | 0
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz nula====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 0 & 0 & 0
| |
| - | \\
| |
| - | 0 & 0 & 0
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz triangular superior''' es toda matriz cuadrada en la que todos los terminos
| |
| - | situados por debajo de la diagonal principal son ceros.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz triangular superior====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & -1 & ~~0
| |
| - | \\
| |
| - | 0 & ~~3 & -1
| |
| - | \\
| |
| - | 0 & ~~0 & ~~2
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz triangular inferior''' es toda matriz cuadrada en la que todos los terminos
| |
| - | situados por encima de la diagonal principal son ceros.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz triangular inferior====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 2 & ~~0 & 0
| |
| - | \\
| |
| - | 3 & -1 & 0
| |
| - | \\
| |
| - | 1 & -1 & 3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz diagonal''' es toda matriz cuadrada en la que todos los terminos
| |
| - | no situados en la diagonal principal son ceros.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz diagonal====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | ~~2 & ~~0 & ~~0
| |
| - | \\
| |
| - | ~~0 & -1 & ~~0
| |
| - | \\
| |
| - | ~~0 & ~~0 & ~~3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz escalar''' es toda matriz diagonal en la que todos los terminos
| |
| - | de la diagonal principal son iguales.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz escalar====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 2 & {0} & {0}
| |
| - | \\
| |
| - | {0} & 2 & {0}
| |
| - | \\
| |
| - | {0} & {0} & 2
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''Matriz unidad''' es la matriz escalar cuyos elementos de la diagonal principal son todos
| |
| - |
| |
| - | <math>
| |
| - | 1
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo: matriz unidad====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & {0} & {0}
| |
| - | \\
| |
| - | {0} & 1 & {0}
| |
| - | \\
| |
| - | {0} & {0} & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
A una matriz cuadrada le podemos asociar un número que, como veremos con posterioridad,
nos permitirá estudiar y resolver un sistema de ecuaciones lineales y examinar si una
matriz dada posee matriz inversa y calcularla.
Este número que vamos a asociar a una matriz cuadrada lo llamaremos determinante de dicha
matriz. Veamos su calculo para matrices cuadradas de orden 2, y con posterioridad
calcularemos determinantes de matrices cuadradas de cualquier orden.
![A =
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
</pre>
<p>\right)
A =
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11} & a_{12}
\\
a_{21} & a_{22}
\end{array}
</pre>
<p>\right)](/images/math/math-6b5b034dbef9fbb4d9ad0eac822a6009.png) se llama determinante de
se llama determinante de
 al número real:
al número real: