Rango de una matriz
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | |||
En una [[¿Qué es una matriz?|matriz]] | En una [[¿Qué es una matriz?|matriz]] | ||
| Línea 26: | Línea 25: | ||
<br/> | <br/> | ||
| - | El '''''rango''''' de una matriz es el número de filas o de columnas | + | El '''''rango''''' de una matriz es el número de filas o de columnas |
| - | [[Dependencia e independencia lineal|linealmente independientes]] que | + | [[Dependencia e independencia lineal|linealmente independientes]] que tieneesa |
| + | matriz. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El rango de una | ||
matriz es, por tanto, siempre menor igual que su numero de filas, y tambien, menor igual | matriz es, por tanto, siempre menor igual que su numero de filas, y tambien, menor igual | ||
que su numero de columnas. Las unicas matrices con rango 0 son las | que su numero de columnas. Las unicas matrices con rango 0 son las | ||
| Línea 37: | Línea 41: | ||
[[Calculo del rango de una matriz por el método de Gauss|método de Gauss]] o | [[Calculo del rango de una matriz por el método de Gauss|método de Gauss]] o | ||
[[Calculo del rango de una matriz por menores|usando menores]]. | [[Calculo del rango de una matriz por menores|usando menores]]. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Calculo del rango de una matriz por el método de Gauss== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Este metodo consiste en transformar la matriz | ||
| + | <math> | ||
| + | \mathbf{A} | ||
| + | \right) | ||
| + | </math> | ||
| + | en una matriz triangular superior mediante las siguientes operaciones: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Operaciones elementales con las filas de una matriz==== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Las operaciones elementales por filas en una matriz son las siguientes: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 1. Intercambiar las filas | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | F_j | ||
| + | </math>. | ||
| + | Esta operación la representaremos así | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | F_i \longleftrightarrow F_j | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 2. Multiplicar la fila | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | por el número | ||
| + | <math> | ||
| + | s \neq 0 | ||
| + | </math> | ||
| + | y sustituir | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | por | ||
| + | <math> | ||
| + | s \cdot F_i | ||
| + | </math>. | ||
| + | Esta operación la representamos de la | ||
| + | siguiente forma: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | s \cdot F_i \longrightarrow F_i | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 3. Sumar las filas | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | F_j | ||
| + | </math>, | ||
| + | multiplicadas por sendos números, | ||
| + | <math> | ||
| + | s | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | t | ||
| + | </math>, | ||
| + | y sustituir | ||
| + | <math> | ||
| + | F_i | ||
| + | </math> | ||
| + | por el resultado de esta suma. Lo representamos así: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | s \cdot F_i + t \cdot F_j \longrightarrow F_i | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Notese que el segundo tipo de operación, | ||
| + | <math> | ||
| + | s \cdot F_i \longrightarrow F_i | ||
| + | </math>, | ||
| + | | ||
| + | es un caso particular de esta última propiedad que se tiene cuando | ||
| + | <math> | ||
| + | t = 0 | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 09:38 3 oct 2010
En una matriz
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png)
podemos considerar sus filas y sus columnas como vectores.
El rango de una matriz es el número de filas o de columnas linealmente independientes que tieneesa matriz.
El rango de una
matriz es, por tanto, siempre menor igual que su numero de filas, y tambien, menor igual que su numero de columnas. Las unicas matrices con rango 0 son las matrices nulas.
El rango de una matriz se puede calcular mediante el método de Gauss o usando menores.
Calculo del rango de una matriz por el método de Gauss
Este metodo consiste en transformar la matriz
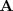 en una matriz triangular superior mediante las siguientes operaciones:
en una matriz triangular superior mediante las siguientes operaciones:
Operaciones elementales con las filas de una matriz
Las operaciones elementales por filas en una matriz son las siguientes:
1. Intercambiar las filas
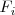 y
y
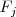 .
Esta operación la representaremos así
.
Esta operación la representaremos así

2. Multiplicar la fila
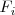 por el número
por el número
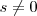 y sustituir
y sustituir
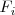 por
por
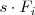 .
Esta operación la representamos de la
siguiente forma:
.
Esta operación la representamos de la
siguiente forma:
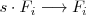
3. Sumar las filas
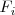 y
y
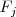 ,
multiplicadas por sendos números,
,
multiplicadas por sendos números,
 y
y
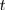 ,
y sustituir
,
y sustituir
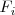 por el resultado de esta suma. Lo representamos así:
por el resultado de esta suma. Lo representamos así:
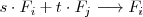
Notese que el segundo tipo de operación,
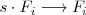 ,
es un caso particular de esta última propiedad que se tiene cuando
,
es un caso particular de esta última propiedad que se tiene cuando
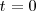 .
.



