¿Qué es una matriz?
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension | Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension | ||
| + | | ||
<math> | <math> | ||
m \times n | m \times n | ||
</math> | </math> | ||
| - | a un conjunto de números reales dispuestos en | + | a un conjunto de números reales dispuestos en |
<math> | <math> | ||
m | m | ||
</math> | </math> | ||
| - | filas y | + | filas y |
<math> | <math> | ||
n | n | ||
</math> | </math> | ||
| - | columnas de la siguiente forma | + | columnas de la siguiente forma |
<br/> | <br/> | ||
| Línea 17: | Línea 18: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left( | |
| - | + | \begin{array}[c]{cccc} | |
| - | + | a_{11 }& a_{12} & \ldots & a_{1n} | |
| - | + | \\ | |
| - | + | a_{21 }& a_{22} & \ldots & a_{2n} | |
| - | + | \\ | |
| - | + | \vdots & \vdots & \ddots & \vdots | |
| - | + | \\ | |
| - | + | a_{m1 }& a_{m2} & \ldots & a_{mn} | |
| - | + | \end{array} | |
| - | + | \right) | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 33: | Línea 34: | ||
<br/> | <br/> | ||
| - | La matriz | + | La matriz |
<math> | <math> | ||
A | A | ||
</math> | </math> | ||
| - | se puede designar tambien como | + | se puede designar tambien como |
<math> | <math> | ||
\quad A = \left( a_{ij} \right) \quad | \quad A = \left( a_{ij} \right) \quad | ||
</math> | </math> | ||
| - | donde | + | donde |
<br/> | <br/> | ||
| Línea 47: | Línea 48: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | \left\{ | |
| - | + | \begin{array}[c]{l} | |
| - | + | i = 1, \, 2, \, \ldots, \, m | |
| + | \\ | ||
| + | j = 1, \, 2, \, \ldots, \, n | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Un elemento generico de la matriz se designa por | ||
| + | <math> | ||
| + | a_{ij} | ||
| + | </math> | ||
| + | en el cual el subindice | ||
| + | <math> | ||
| + | i | ||
| + | </math> | ||
| + | representa el numero de fila que ocupa el elemento y el subindice | ||
| + | <math> | ||
| + | j | ||
| + | </math> | ||
| + | el numero de columna. | ||
| + | |||
| + | El conjunto de matrices de dimension | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | se denota por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | M_{m \times n} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El conjunto de matrices de dimension | ||
| + | <math> | ||
| + | n \times n | ||
| + | </math> | ||
| + | , tambien llamadas de orden | ||
| + | <math> | ||
| + | n | ||
| + | </math> | ||
| + | , se denota por: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | M_n | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos: | ||
| + | |||
| + | * la diagonal principal formada por los elementos de la forma | ||
| + | <math> | ||
| + | a_{ii} | ||
| + | </math> | ||
| + | | ||
| + | |||
| + | * la diagonal secundaria formada por los elementos de la forma | ||
| + | <math> | ||
| + | a_{ij} | ||
| + | </math> | ||
| + | tales que | ||
| + | <math> | ||
| + | i + j = n + 1 | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}[c]{cc} | ||
| + | \left( | ||
| + | \begin{array}[c]{cccc} | ||
| + | \mathbf{a_{11}} & a_{12} & a_{13} & a_{14} | ||
\\ | \\ | ||
| - | + | a_{21} & \mathbf{a_{22}} & a_{23} & a_{24} | |
| + | \\ | ||
| + | a_{31} & a_{32} & \mathbf{a_{33}} & a_{34} | ||
| + | \\ | ||
| + | a_{41} & a_{42} & a_{43} & \mathbf{a_{44}} | ||
\end{array} | \end{array} | ||
| - | \right | + | \right) |
| + | & | ||
| + | \left( | ||
| + | \begin{array}[c]{cccc} | ||
| + | a_{11} & a_{12} & a_{13} & \mathbf{a_{14}} | ||
| + | \\ | ||
| + | a_{21} & a_{22} & \mathbf{a_{23}} & a_{24} | ||
| + | \\ | ||
| + | a_{31} & \mathbf{a_{32}} & a_{33} & a_{34} | ||
| + | \\ | ||
| + | \mathbf{a_{41}} & a_{42} & a_{43} & a_{44} | ||
| + | \end{array} | ||
| + | \right) | ||
| + | \\ | ||
| + | & | ||
| + | \\ | ||
| + | \makebox{Diagonal principal} & \makebox{Diagonal secundaria} | ||
| + | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
Revisión de 23:07 27 nov 2006
Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension
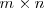 a un conjunto de números reales dispuestos en
a un conjunto de números reales dispuestos en
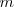 filas y
filas y
 columnas de la siguiente forma
columnas de la siguiente forma
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png)
La matriz
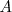 se puede designar tambien como
se puede designar tambien como
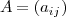 donde
donde
![\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.](/images/math/math-22d889e2bbcf6ec56d6db3849ebbe730.png)
Un elemento generico de la matriz se designa por
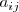 en el cual el subindice
en el cual el subindice
 representa el numero de fila que ocupa el elemento y el subindice
representa el numero de fila que ocupa el elemento y el subindice
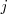 el numero de columna.
el numero de columna.
El conjunto de matrices de dimension
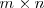 se denota por:
se denota por:
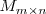
El conjunto de matrices de dimension
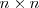 , tambien llamadas de orden
, tambien llamadas de orden
 , se denota por:
, se denota por:
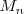
Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
- la diagonal principal formada por los elementos de la forma
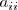
- la diagonal secundaria formada por los elementos de la forma
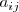 tales que
tales que
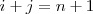
![\begin{array}[c]{cc}
</p>
<pre> \left(
\begin{array}[c]{cccc}
\mathbf{a_{11}} & a_{12} & a_{13} & a_{14}
\\
a_{21} & \mathbf{a_{22}} & a_{23} & a_{24}
\\
a_{31} & a_{32} & \mathbf{a_{33}} & a_{34}
\\
a_{41} & a_{42} & a_{43} & \mathbf{a_{44}}
\end{array}
\right)
&
\left(
\begin{array}[c]{cccc}
a_{11} & a_{12} & a_{13} & \mathbf{a_{14}}
\\
a_{21} & a_{22} & \mathbf{a_{23}} & a_{24}
\\
a_{31} & \mathbf{a_{32}} & a_{33} & a_{34}
\\
\mathbf{a_{41}} & a_{42} & a_{43} & a_{44}
\end{array}
\right)
\\
&
\\
\makebox{Diagonal principal} & \makebox{Diagonal secundaria}
</pre>
<p>\end{array}
\begin{array}[c]{cc}
</p>
<pre> \left(
\begin{array}[c]{cccc}
\mathbf{a_{11}} & a_{12} & a_{13} & a_{14}
\\
a_{21} & \mathbf{a_{22}} & a_{23} & a_{24}
\\
a_{31} & a_{32} & \mathbf{a_{33}} & a_{34}
\\
a_{41} & a_{42} & a_{43} & \mathbf{a_{44}}
\end{array}
\right)
&
\left(
\begin{array}[c]{cccc}
a_{11} & a_{12} & a_{13} & \mathbf{a_{14}}
\\
a_{21} & a_{22} & \mathbf{a_{23}} & a_{24}
\\
a_{31} & \mathbf{a_{32}} & a_{33} & a_{34}
\\
\mathbf{a_{41}} & a_{42} & a_{43} & a_{44}
\end{array}
\right)
\\
&
\\
\makebox{Diagonal principal} & \makebox{Diagonal secundaria}
</pre>
<p>\end{array}](/images/math/math-b55d3ab2d5b012a0fa6f3b9542f554e5.png)



