Efecto Doppler
De Wikillerato
(→Foco emisor en movimiento, observador y medio en reposo) |
|||
| (44 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
El efecto Doppler es un fenómeno común a todos los movimientos ondulatorios, aunque su observación es particularmente fácil en las ondas sonoras y en las ondas electromagnéticas, como se verá en su lugar. El fenómeno se observará en tanto la velocidad del foco emisor sea muy pequeña frente a la velocidad de propagación de las ondas. | El efecto Doppler es un fenómeno común a todos los movimientos ondulatorios, aunque su observación es particularmente fácil en las ondas sonoras y en las ondas electromagnéticas, como se verá en su lugar. El fenómeno se observará en tanto la velocidad del foco emisor sea muy pequeña frente a la velocidad de propagación de las ondas. | ||
| + | [[Imagen:Christian_Doppler.jpg|Christian Doppler]] | ||
Hasta ahora hemos supuesto que tanto el foco emisor como el observador se encontraban permanentemente en reposo así como el medio en el que se producen las ondas. Sin embargo, en un instante o intervalo de tiempo determinado, pueden encontrarse en movimiento uno, dos o los tres. La consecuencia de cualquiera de estos posibles movimientos es un '''''cambio de frecuencia de las ondas percibidas por el observador.''''' | Hasta ahora hemos supuesto que tanto el foco emisor como el observador se encontraban permanentemente en reposo así como el medio en el que se producen las ondas. Sin embargo, en un instante o intervalo de tiempo determinado, pueden encontrarse en movimiento uno, dos o los tres. La consecuencia de cualquiera de estos posibles movimientos es un '''''cambio de frecuencia de las ondas percibidas por el observador.''''' | ||
| Línea 8: | Línea 9: | ||
===Foco emisor en movimiento, observador y medio en reposo=== | ===Foco emisor en movimiento, observador y medio en reposo=== | ||
| - | |||
| - | + | <div style="border: 1px solid #aaaaaa; width:550px;"><flash>file=AnimacionEfectoDoppler.swf|width=550|height=300|quality=best</flash></div> | |
| - | |||
| - | + | Supongamos que un foco emisor <math> F </math>, que emite ondas cuya velocidad de propagación es v, se mueve con respecto al observador <math> O </math> con una velocidad <math>\nu_F</math>. Consideremos positivas las velocidades si se mueven hacia el observador y negativas si lo hacen en sentido contrario. | |
| - | + | En un tiempo <math>t</math>, la onda recorre una longitud <math> x </math> = <math> \nu t</math>, acercándose al observador hasta el punto <math> B </math>. | |
| - | <math> | + | |
| - | + | ||
| - | <math> \frac{ | + | [[Imagen:Efecto-Doppler-1.jpg]] |
| - | <math> {v}{\ | + | |
| - | <math> \ | + | Si el foco emisor <math>F</math> se acerca, durante ese mismo tiempo <math>t</math> se ha desplazado <math>x_F = \nu_F t</math> , llegando hasta el punto <math>A</math>. |
| + | |||
| + | Durante ese tiempo <math>F</math> ha emitido un número de ondas igual a <math>\frac{t}{T}=f.t</math>. | ||
| + | |||
| + | Estas ondas se encuentran comprimidas dentro de la distancia <math>AB </math>, y la distancia entre las ondas será la longitud de onda aparente <math>\lambda '</math>de las ondas percibidas por el observador. | ||
| + | |||
| + | <math>\lambda ' = \frac{FB - FA}{f t}</math> = <math> \frac{\nu t - \nu_F t}{ft}</math> = <math>\frac{\nu -\nu_F}{f}</math> | ||
| + | |||
| + | Pero la ecuación <math>v = \lambda f</math> , se cumplirá siempre, en este caso, si es <math>f_o</math> la frecuencia de las ondas percibida por el observador tendremos <math>\nu = \lambda ' f_{o}</math>, con lo cual, | ||
| + | |||
| + | <math> \frac {v} {f_o}</math> = <math>\frac{\nu - \nu_F}{f}</math> | ||
| + | |||
| + | <math> {v}{f_o}</math> = <math>\frac{\nu - \nu_F}{f}</math> | ||
| + | |||
| + | <math>f_o</math> = <math> \frac {\nu} {\nu - \nu_F} f </math> | ||
| + | |||
| + | Frecuencia percibida <math>f_o > f</math> Frecuencia de las ondas emitidas | ||
| + | |||
| + | <math>\lambda ' < \lambda</math> disminuye la longitud de onda aparente. | ||
| + | |||
| + | Si el foco emisor se aleja del observador, su velocidad <math>\nu_F < 0</math> puesto que su velocidad tendrá sentido contrario al de las ondas que llegan al observador. | ||
| + | |||
| + | Cambiando el signo de <math>\nu_F</math> tendremos, | ||
| + | |||
| + | <math> f_o = \frac {\nu}{\nu + \nu_F} f </math> | ||
| + | |||
| + | Frecuencia percibida <math>f_o < f </math> Frecuencia emitida. | ||
| + | |||
| + | <math>\lambda ' > \lambda</math> aumenta la longitud de onda aparente. | ||
| + | |||
| + | ===Observador en movimiento, foco emisor y medio en reposo=== | ||
| + | |||
| + | Si el observador se moviera con una velocidad vO alejándose del foco emisor F, la distancia entre los frentes de onda no se altera, sin embargo, el número de frentes que percibe en un tiempo t es menor, por lo cual la frecuencia aparente disminuye. | ||
| + | Si el observador hubiera permanecido en reposo, en un tiempo t habría recibido todas las ondas comprendidas en el segmento <math>x</math>=<math>\nu t</math>, ese número es | ||
| + | |||
| + | <math> \frac{x}{\lambda} = \frac{\nu t}{\lambda}</math> | ||
| + | |||
| + | [[Imagen:Efecto-Doppler-2.jpg]] | ||
| + | |||
| + | Pero el observador se ha alejado una distancia <math> x_o = v_o t</math>, llegando hasta el punto <math>C</math> y sólo percibirá las ondas comprendidas entre <math>B</math> y <math> O </math>, es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse. | ||
| + | |||
| + | <math>\frac{\nu}{\lambda '} = \frac {\nu - \nu_o}{\lambda}</math> | ||
| + | |||
| + | <math> \frac{1}{\lambda '} = \frac {\nu - \nu_o}{\nu} \frac {1}{\lambda}</math> | ||
| + | |||
| + | <math> f_o = \frac {\nu-\nu_o}{\nu} f </math> | ||
| + | |||
| + | Frecuencia percibida <math>f_o < f</math> frecuencia de las ondas emitidas | ||
| + | |||
| + | La longitud de onda aparente <math>\lambda ' > \lambda</math> longitud de onda de las ondas emitidas | ||
| + | |||
| + | Si el observador se acerca al foco emisor, el número de frentes que percibe es mayor que si permaneciera en reposo. Para los cálculos basta cambiar de signo a la velocidad del observador <math>\nu_o</math> puesto que <math> O </math> se mueve en sentido contrario al del movimiento del frente de ondas que le llega. | ||
| + | |||
| + | <math> f_o = \frac{\nu + \nu_o}{v} f</math> | ||
| + | |||
| + | Frecuencia percibida <math> f_o > f </math> frecuencia de las ondas emitidas. | ||
| + | |||
| + | La longitud de onda aparente <math>\lambda ' < \lambda</math> longitud de onda de las ondas emitidas. | ||
| + | |||
| + | ===Foco emisor y observador en movimiento, medio en reposo=== | ||
| + | |||
| + | En el caso en que se movieran simultáneamente el foco y el observador, aunque con distintas velocidades tendríamos: | ||
| + | |||
| + | <math>f_o = \frac {\nu}{\nu - \nu_F} f </math> | ||
| + | |||
| + | Ahora bien, la frecuencia de las ondas <math> f </math> que aparece en la ecuación, disminuye como consecuencia del movimiento del observador, y esa <math> f </math> habrá de ser sustituida por | ||
| + | |||
| + | <math>f'_o = \frac {\nu - \nu_o}{v} f </math>, en consecuencia tendremos: | ||
| + | |||
| + | <math>f_o = \frac {\nu}{\nu - \nu_F} \frac {\nu - \nu_o}{\nu} f </math> | ||
| + | |||
| + | Con lo cual queda, | ||
| + | |||
| + | <math> f_o = \frac {\nu - \nu_o}{\nu - \nu_F} f </math> | ||
| + | |||
| + | Puede observarse que si <math>\nu_F = \nu_o</math> no se produce cambio de frecuencia, las ondas ''alcanzan'' al observador siempre en número constante. | ||
| + | |||
| + | ===Aplicaciones=== | ||
| + | |||
| + | La policía de tráfica usa este principio para determinar la velocidad de un móvil. Si la policía se encuentra en reposo y emite ondas electromagneticas de baja frecuencia, estas ondas se reflejarán en el móvil y la onda reflejada tendrá una frecuencia diferente según la velocidad del móvil. | ||
| + | |||
| + | Este principio también se ha analizado en el '''''sonar''''' de los barcos para determinar la posición de objetos submarinos. | ||
| + | |||
| + | Ya veremos como nos permite afirmar que el universo se encuentra en la actualidad en fase de expansión. | ||
| + | |||
| + | ==Ondas de Choque== | ||
| + | |||
| + | Si la velocidad del foco se acerca a la velocidad de propagación de las ondas en el medio, el frente de ondas se deforma y no valen los análisis para el efecto Doppler. En el caso de que esas velocidades se hagan iguales, la energía se agrupa en direcciones que forman ángulos muy pequeños con la dirección del movimiento del foco. Este efecto explica el estampido asociado a los aviones cuando sus velocidades se hacen superiores a las del sonido. | ||
| + | |||
| + | Si la velocidad del foco es mayor que la velocidad de fase de las ondas se produce una '''''onda de choque''''' que es diferente de las ondas ordinarias. | ||
| + | |||
| + | [[Categoría:Física]] | ||
Revisión actual
El efecto Doppler es un fenómeno común a todos los movimientos ondulatorios, aunque su observación es particularmente fácil en las ondas sonoras y en las ondas electromagnéticas, como se verá en su lugar. El fenómeno se observará en tanto la velocidad del foco emisor sea muy pequeña frente a la velocidad de propagación de las ondas.
Hasta ahora hemos supuesto que tanto el foco emisor como el observador se encontraban permanentemente en reposo así como el medio en el que se producen las ondas. Sin embargo, en un instante o intervalo de tiempo determinado, pueden encontrarse en movimiento uno, dos o los tres. La consecuencia de cualquiera de estos posibles movimientos es un cambio de frecuencia de las ondas percibidas por el observador.
Tabla de contenidos |
Estudio Analítico
Foco emisor en movimiento, observador y medio en reposo
Supongamos que un foco emisor 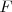 , que emite ondas cuya velocidad de propagación es v, se mueve con respecto al observador
, que emite ondas cuya velocidad de propagación es v, se mueve con respecto al observador 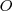 con una velocidad
con una velocidad 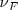 . Consideremos positivas las velocidades si se mueven hacia el observador y negativas si lo hacen en sentido contrario.
. Consideremos positivas las velocidades si se mueven hacia el observador y negativas si lo hacen en sentido contrario.
En un tiempo 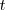 , la onda recorre una longitud
, la onda recorre una longitud  =
= 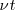 , acercándose al observador hasta el punto
, acercándose al observador hasta el punto 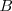 .
.
Si el foco emisor 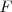 se acerca, durante ese mismo tiempo
se acerca, durante ese mismo tiempo 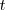 se ha desplazado
se ha desplazado 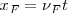 , llegando hasta el punto
, llegando hasta el punto 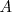 .
.
Durante ese tiempo 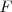 ha emitido un número de ondas igual a
ha emitido un número de ondas igual a 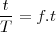 .
.
Estas ondas se encuentran comprimidas dentro de la distancia 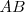 , y la distancia entre las ondas será la longitud de onda aparente
, y la distancia entre las ondas será la longitud de onda aparente 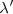 de las ondas percibidas por el observador.
de las ondas percibidas por el observador.
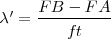 =
= 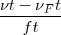 =
= 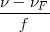
Pero la ecuación 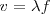 , se cumplirá siempre, en este caso, si es
, se cumplirá siempre, en este caso, si es 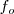 la frecuencia de las ondas percibida por el observador tendremos
la frecuencia de las ondas percibida por el observador tendremos 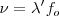 , con lo cual,
, con lo cual,
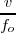 =
= 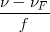
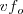 =
= 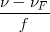
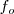 =
= 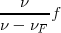
Frecuencia percibida  Frecuencia de las ondas emitidas
Frecuencia de las ondas emitidas
 disminuye la longitud de onda aparente.
disminuye la longitud de onda aparente.
Si el foco emisor se aleja del observador, su velocidad 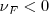 puesto que su velocidad tendrá sentido contrario al de las ondas que llegan al observador.
puesto que su velocidad tendrá sentido contrario al de las ondas que llegan al observador.
Cambiando el signo de 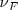 tendremos,
tendremos,
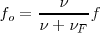
Frecuencia percibida  Frecuencia emitida.
Frecuencia emitida.
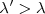 aumenta la longitud de onda aparente.
aumenta la longitud de onda aparente.
Observador en movimiento, foco emisor y medio en reposo
Si el observador se moviera con una velocidad vO alejándose del foco emisor F, la distancia entre los frentes de onda no se altera, sin embargo, el número de frentes que percibe en un tiempo t es menor, por lo cual la frecuencia aparente disminuye.
Si el observador hubiera permanecido en reposo, en un tiempo t habría recibido todas las ondas comprendidas en el segmento  =
=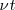 , ese número es
, ese número es
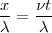
Pero el observador se ha alejado una distancia 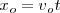 , llegando hasta el punto
, llegando hasta el punto 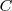 y sólo percibirá las ondas comprendidas entre
y sólo percibirá las ondas comprendidas entre 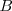 y
y 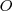 , es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse.
, es decir las que percibiría en el caso de permanecer en reposo menos las que deja de percibir por alejarse.
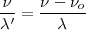
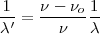
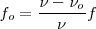
Frecuencia percibida  frecuencia de las ondas emitidas
frecuencia de las ondas emitidas
La longitud de onda aparente 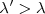 longitud de onda de las ondas emitidas
longitud de onda de las ondas emitidas
Si el observador se acerca al foco emisor, el número de frentes que percibe es mayor que si permaneciera en reposo. Para los cálculos basta cambiar de signo a la velocidad del observador 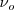 puesto que
puesto que 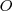 se mueve en sentido contrario al del movimiento del frente de ondas que le llega.
se mueve en sentido contrario al del movimiento del frente de ondas que le llega.
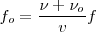
Frecuencia percibida  frecuencia de las ondas emitidas.
frecuencia de las ondas emitidas.
La longitud de onda aparente  longitud de onda de las ondas emitidas.
longitud de onda de las ondas emitidas.
Foco emisor y observador en movimiento, medio en reposo
En el caso en que se movieran simultáneamente el foco y el observador, aunque con distintas velocidades tendríamos:
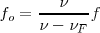
Ahora bien, la frecuencia de las ondas 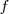 que aparece en la ecuación, disminuye como consecuencia del movimiento del observador, y esa
que aparece en la ecuación, disminuye como consecuencia del movimiento del observador, y esa 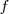 habrá de ser sustituida por
habrá de ser sustituida por
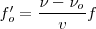 , en consecuencia tendremos:
, en consecuencia tendremos:
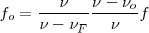
Con lo cual queda,
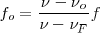
Puede observarse que si 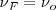 no se produce cambio de frecuencia, las ondas alcanzan al observador siempre en número constante.
no se produce cambio de frecuencia, las ondas alcanzan al observador siempre en número constante.
Aplicaciones
La policía de tráfica usa este principio para determinar la velocidad de un móvil. Si la policía se encuentra en reposo y emite ondas electromagneticas de baja frecuencia, estas ondas se reflejarán en el móvil y la onda reflejada tendrá una frecuencia diferente según la velocidad del móvil.
Este principio también se ha analizado en el sonar de los barcos para determinar la posición de objetos submarinos.
Ya veremos como nos permite afirmar que el universo se encuentra en la actualidad en fase de expansión.
Ondas de Choque
Si la velocidad del foco se acerca a la velocidad de propagación de las ondas en el medio, el frente de ondas se deforma y no valen los análisis para el efecto Doppler. En el caso de que esas velocidades se hagan iguales, la energía se agrupa en direcciones que forman ángulos muy pequeños con la dirección del movimiento del foco. Este efecto explica el estampido asociado a los aviones cuando sus velocidades se hacen superiores a las del sonido.
Si la velocidad del foco es mayor que la velocidad de fase de las ondas se produce una onda de choque que es diferente de las ondas ordinarias.
Tweet





