Cálculo de la inversa de una matriz
De Wikillerato
La matriz inversa de una matriz cuadrada
 de orden
de orden
 , es la matriz,
, es la matriz,
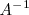 , de orden
, de orden
 que verifica:
que verifica:
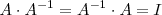
Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices singulares.
Antes de calcular la matriz inversa de una dada hemos de asegurarnos de que efectivamente existe la matriz inversa. Para ello utilizamos la siguiente propiedad:
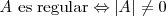
Una vez que hemos asegurado la existencia de la matriz inversa, calculamos esta mediante la siguiente expresion:
donde
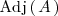 es la matriz adjunta de
es la matriz adjunta de
 . Se verifica que
. Se verifica que
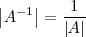


![A^{-1} = \frac{1}{\left| A \right|} \cdot
\left[
\makebox{Adj}
\left(
\, A \,
\right)
\right]
^t
A^{-1} = \frac{1}{\left| A \right|} \cdot
\left[
\makebox{Adj}
\left(
\, A \,
\right)
\right]
^t](/images/math/math-f567befc24c749b340e529b2c5d18d12.png)

